Allgemeine Definition von statistischer Abhängigkeit (1)
Bisher haben wir die statistische Abhängigkeit zwischen Ereignissen nicht besonders beachtet, auch wenn wir sie wie im Fall zweier disjunkter Mengen bereits verwendet haben: Gehört ein Element zu $A$, so kann es mit Sicherheit nicht auch in der disjunkten Menge $B$ enthalten sein.
Die stärkste Form von Abhängigkeit überhaupt ist eine deterministische Abhängigkeit zwischen zwei Mengen bzw. zwei Ereignissen. Weniger ausgeprägt ist die statistische Abhängigkeit. Beginnen wir mit deren Komplement:
Zwei Ereignisse $A$ und $B$ bezeichnet man dann als statistisch unabhängig (englisch: statistical independent) , wenn die Wahrscheinlichkeit der Schnittmenge $A ∩ B$ gleich dem Produkt der Einzelwahrscheinlichkeiten ist: $$\rm Pr(\it A \cap \it B) = \rm Pr(\it A)\cdot \rm Pr(\it B).$$
In manchen Anwendungsfällen ist die statistische Unabhängigkeit offensichtlich, zum Beispiel beim Experiment Münzwurf. Die Wahrscheinlichkeit für Zahl oder Bild ist unabhängig davon, ob beim letzten Wurf Zahl oder Bild aufgetreten ist. Und auch die einzelnen Ergebnisse beim Zufallsexperiment Werfen einer Roulettekugel sind bei fairen Bedingungen stets statistisch unabhängig voneinander, auch wenn einzelne Systemspieler dies nicht wahrhaben wollen.
Bei anderen Anwendungen ist dagegen die Frage, ob zwei Ereignisse statistisch unabhängig sind oder nicht, gefühlsmäßig nicht oder nur sehr schwer zu beantworten. Hier kann man nur durch Überprüfung des oben angegebenen formalen Unabhängigkeitskriteriums zur richtigen Antwort gelangen, wie das Beispiel auf der nächsten Seite zeigen soll.
Allgemeine Definition von statistischer Abhängigkeit (2)
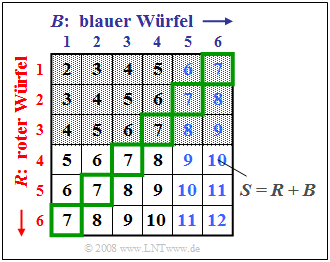
Wir betrachten wieder das Zufallsexperiment Werfen mit zwei Würfeln, wobei die beiden Würfel an ihren Farben Rot $(R)$ und Blau $(B)$ unterschieden werden können. Die Grafik soll diesen Sachverhalt verdeutlichen, wobei in dem zweidimensionalen Feld $(R, B)$ die Summe $S = R + B$ eingetragen ist.
Die Grafik kann wie folgt interpretiert werden:
- Die beiden Ereignisse $A_1 = „R < 4”$ und $A_2 = „B > 4”$ sind im Bild durch rötlichen Hintergrund bzw. blaue Zahlen hervorgehoben. $A_1$ und $A_2$ sind statistisch unabhängig, da die Wahrscheinlichkeit der Schnittmenge – also Pr( $A_1 ∩ A_2$) = 1/6 – gleich dem Produkt der beiden Einzelwahrscheinlichkeiten Pr( $A_1$) = 1/2 und Pr( $A_2$) = 1/3 ist. Aufgrund der Aufgabenstellung hätte auch jedes andere Ergebnis sehr überrascht.
- Aber auch die beiden Ereignisse $A_1 = „R < 4”$ und $A_3 = „S = 7”$ sind wegen Pr( $A_1$) = 1/2, Pr( $A_3$) = 1/6 und Pr( $A_1 ∩ A_3$) = 1/12 statistisch voneinander unabhängig. Das Ereignis $„S =$ 7” ist in der Grafik durch grüne Umrahmungen gekennzeichnet.
- Dagegen bestehen wegen Pr( $A_1$) = 1/2, Pr( $A_4$) = 5/36 und Pr( $A_1 ∩ A_4$) = 1/18 statistische Bindungen zwischen $A_1 = „R < 4”$ und dem im Bild auf der nächsten Seite markierten Ereignis $A_4 = „S = 8”$. Die beiden Ereignisse $A_1 = „R < 4”$ und $A_5 = „S ≥ 10”$ sind sogar disjunkt. Dies zeigt, dass Disjunktivität eine besonders ausgeprägte Form von statistischer Abhängigkeit ist.