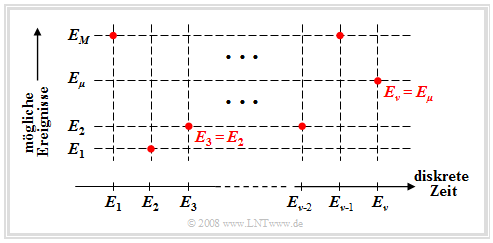
Betrachtetes Szenario
Wir betrachten nun abschließend den Fall, dass man ein Experiment fortlaufend durchführt und zu jedem diskreten Zeitpunkt $ν =$ 1, 2, 3, ….. ein Ereignis $E_ν$ eintritt. Hierbei soll gelten: $$E_\nu \in G = \{ E_{\rm 1}, E_{\rm 2}, \hspace{0.1cm}...\hspace{0.1cm}, E_\mu , \hspace{0.1cm}...\hspace{0.1cm}, E_M \}.$$
Diese mathematisch nicht ganz saubere Nomenklatur bedeutet (siehe nachfolgende Grafik):
- Die $M$ möglichen Ereignisse werden mit dem Laufindex $μ$ durchnummeriert.
- Der Index $ν$ benennt die diskreten Zeitpunkte, zu denen Entscheidungen gefällt werden.
Zur einfacheren Darstellung beschränken wir uns im Folgenden auf den Fall $M =$ 2 mit der Grundmenge $G$ = { $A, B$}. Wir berücksichtigen, dass die Wahrscheinlichkeit des Ereignisses $E_ν$ durchaus von allen vorherigen Ereignissen – also von $E_{ν–1}, E_{ν–2}, E_{ν–3}$, . . . – abhängen kann. Das bedeutet auch, dass wir eine Ereignisfolge mit inneren statistischen Bindungen betrachten.
Dieses Szenario ist ein Sonderfall eines zeit- und wertdiskreten Zufallsprozesses. Solche Prozesse werden in Kapitel 4.4 noch ausführlich behandelt.
Aus einem Kartenstapel mit 32 Karten (darunter 4 Asse) werden nacheinander Karten gezogen. Mit den Ereignissen $A =$ „die gezogene Karte ist ein Ass” und $B =$ „die gezogene Karte ist kein Ass” lauten die Wahrscheinlichkeiten zum Zeitpunkt $ν =$ 1: $${\rm Pr} (A_{\rm 1}) = \frac{4}{32}= \frac{1}{8}; \hspace{0.5cm}{\rm Pr} (B_{\rm 1}) = \frac{28}{32}= \frac{7}{8}.$$
Die Wahrscheinlichkeit Pr( $A_2$), dass zur Zeit $ν =$ 2 ein Ass gezogen wird, hängt nun davon ab,
- ob zum Zeitpunkt $ν =$ 1 ein Ass gezogen wurde ⇒ Pr( $A_2$) = 3/31 < 1/8, oder
- ob zum Zeitpunkt $ν =$ 1 kein Ass gezogen wurde ⇒ Pr( $A_2$) = 4/31 > 1/8.
Auch die Wahrscheinlichkeiten Pr( $A_ν$) zu späteren Zeitpunkten ν hängen stets vom Eintreffen bzw. Nichteintreffen aller vorherigen Ereignisse $E_1 ... E_{ν–1}$ ab.