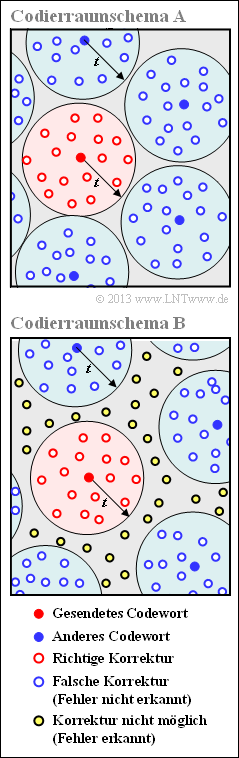
Exercise 2.16: Bounded Distance Decoding: Decision Regions

Betrachtete Codierraumschemata

Considered coding space schemes

We assume a block code of length $n$ with symbols $c_i ∈ {\rm GF}(2^m)$ that can correct up to $t$ symbols. Each possible received word $\underline{y}_i$ can then be viewed as a point in a high-dimensional space. Assuming the basis ${\rm GF}(2) = \{0, \, 1\}$ the dimension $n is \cdot m$.

The diagram shows such a space in simplified, schematic two dimensional representation.

The illustration is to be interpreted as follows:

The red dot $\underline{c}_j$ was sent. All red outlined points $\underline{y}_i$ in a hypersphere around this point $\underline{c}_j$ with the parameter $t$ as radius can be corrected. Using the nomenclature according to the "graph" in the theory section, then $\underline{z}_i = \underline{c}_j$
⇒ "Error correction is successful".

For very many symbol errors, $\underline{c}_j$ may be corrupted into a blue (or white-blue) dot $\underline{y}_j$ belonging to the hyper-sphere of another code word $\underline{c}_{k ≠ j}$ . In this case the decoder makes a wrong decision
⇒ "The received word $\underline{y}_j$ is decoded incorrectly".

Finally, as in the sketch below, there may be yellow dots that do not belong to any hypersphere
⇒ "The received word $\underline{y}_j$ is not decodable".

In this exercise you are to decide which of the two code space schemes is suitable for describing

Hints:

The exercise complements the topic of the chapter "Error Probability and Application Areas".
It is intended to illustrate significant differences in decoding Reed–Solomon codes and Hamming codes.

Questions

Solution

(1) Correct is solution 1, since the coding space scheme $\rm A$ describes a perfect code and each Hamming code $(n, \, k, \, 3)$ is a perfect code:

For any Hamming code $(n, \, k, \, 3)$, there are a total of $2^n$ possible received words $\underline{y}_i$, which are assigned to one of $2^k$ possible code words $\underline{c}_j$ during syndrome decoding.
Because of the HC property $d_{\rm min} = 3$, all spheres in $n$ dimensional space have radius $t = 1$. Thus in all spheres there are $2^{n-k}$ points, for example.

$\text{HC (7, 4, 3)}$: one point for error-free transmission and seven points for a bit error ⇒ $1 + 7 = 8 = 2^3 = 2^{7-4}$.
$\text{HC (15, 11, 3)}$: one point for error-free transmission and now 15 points for a bit error ⇒ $1 + 15 = 16 = 2^4 = 2^{15-11}$.

Note: Since the Hamming code is a binary code, here the code space has the dimension $n$.

(2) Correct is answer 1:

In the gray area outside "spheres" there is not a single point in a perfect code.
This was also shown in the calculation for subtask (1).

(3) The Reed–Solomon codes are described by the coding space scheme $\rm B$ ⇒ Answer 2.

Here there are numerous yellow points in the gray area, i.e. points that cannot be assigned to any sphere in Bounded Distance Decoding (BDD).
For example, if we consider the $\rm RSC \, (7, \, 3, \, 5)_8$ with code parameters $n = 7, \, k = 3$ and $t = 2$, there are a total of $8^7 = 2097152$ points and $8^3 = 512$ hypersphere here.
If this code were perfect, then there should be $8^4 = 4096$ points within each sphere. However, it holds:

$${\rm Pr}(\underline{\it y}_{\it i} {\rm \hspace{0.1cm}lies\hspace{0.1cm} within\hspace{0.1cm} the\hspace{0.1cm} red\hspace{0.1cm} sphere)} = {\rm Pr}(f \le t) = {\rm Pr}(f = 0)+ {\rm Pr}(f = 1)+{\rm Pr}(f = 2) =1 + {7 \choose 1} \cdot 7 + {7 \choose 2} \cdot 7^2 = 1079 \hspace{0.05cm}.$$

For ${\rm Pr}(f = 1)$ it is considered that there can be "$7 \rm \ over \ 1$" $= 7$ error positions, and for each error position also seven different error values. The same is considered for ${\rm Pr}(f = 2)$.

(4) Correct is answer 3:

A point in gray no-man's land is reached with fewer symbol errors than a point in another hypersphere.
For long codes, an upper bound on the corruption probability is given in the literature:

$${\rm Pr}(\underline{y}_{i} {\rm \hspace{0.15cm}wird\hspace{0.15cm} falsch\hspace{0.15cm} decodiert)} = {\rm Pr}(\underline{z} \ne \underline{c}) \le \frac{1}{t\hspace{0.05cm}!} \hspace{0.05cm}.$$

For the ${\rm RSC} \, (225, \, 223, \, 33)_{256} \ \Rightarrow \ t = 16$, this upper bound yields the value $1/(16!) < 10^{-14}$.

	The probability ${\rm Pr}(\underline{y} \rm \ is \ not \ decodable)$ is exactly zero.
	${\rm Pr}(\underline{y} \rm \ is \ not \ decodable)$ is nonzero, but negligible.
	It holds ${\rm Pr}(\underline{y} {\rm \ is \ not \ decodable}) > {\rm Pr}(\underline{y} \rm \ is \ incorrectly \ decoded)$.