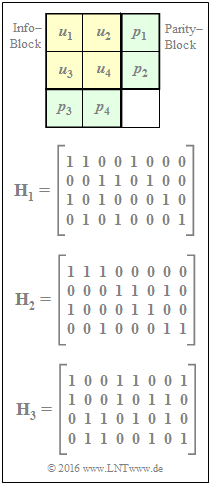
Exercise 4.11: Analysis of Parity-check Matrices

Product code described by the parity-check matrix $\mathbf{H}$

In the adjacent graphic, a product code is indicated at the top, which is characterized by the following parity-check equations:

$$p_1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_2\hspace{0.05cm},$$

$$p_2 = u_3 \oplus u_4\hspace{0.05cm},$$

$$p_3 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_1 \oplus u_3\hspace{0.05cm},$$

$$p_4 = u_2 \oplus u_4\hspace{0.05cm}.$$

Below are given the check matrices $\mathbf{H}_1, \ \mathbf{H}_2$ and $\mathbf{H}_3$. To be checked: Which of the matrices correctly describe the given product code according to the equation $\underline{x} = \underline{u} \cdot \mathbf{H}^{\rm T}$ assuming the following definitions:

the code word $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$,

the code word $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.

All $\mathbf{H}$ matrices contain fewer "ones" than "zeros". This is a characteristic of the so-called "low–density parity–check codes" $($short: $\rm LDPC$ codes$)$. In the case of LDPC codes relevant to practice, however, the share of "ones" is still significantly lower than in these examples.

Furthermore, note for the exercise:

An $(n, \ k)$ $\underline{x} = \underline{u} \cdot \mathbf{H}^{\rm T}$ block code is systematic if the first $k$ bits of the code word $\underline{x}$ contains the information word $\underline{u}$. With the code word $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$ the parity-check matrix $\mathbf{H}$ must then end with a $k × k$ diagonal matrix.

A "regular code" $($with respect to the LDPC application$)$ exists, if the Hamming weight of all rows ⇒ $w_{\rm R}$ and the Hamming weight of all columns ⇒ $w_{\rm C}$ are equal in each case. Otherwise, one speaks of an "irregular LDPC code".

The parity-check matrix $\mathbf{H}$ of a conventional linear $(n, \ k)$ block code consists of exactly $m = n - k$ rows and $n$ columns. For LDPC codes, the requirement is $m ≥ n - k$. The equal sign is true if the $m$ parity-check equations are statistically independent.

From the parity-check matrix $\mathbf{H}$ a lower bound for the code rate $R$ can be given:

$$R \ge 1 - \frac{{\rm E}[w_{\rm C}]}{{\rm E}[w_{\rm R}]} \hspace{0.5cm}{\rm with}\hspace{0.5cm} {\rm E}[w_{\rm C}] =\frac{1}{n} \cdot \sum_{i = 1}^{n}w_{\rm C}(i) \hspace{0.5cm}{\rm and}\hspace{0.5cm} {\rm E}[w_{\rm R}] =\frac{1}{m} \cdot \sum_{j = 1}^{ m}w_{\rm R}(j) \hspace{0.05cm}.$$

This equation applies equally to regular and irregular LDPC codes, where for regular codes holds ${\rm E}[w_{\rm C}] = w_{\rm C}$ and ${\rm E}[w_{\rm R}] = w_{\rm R}$.

Hints:

This exercise belongs to the chapter "Basics of the Low–density Parity–check".

Reference is made in particular to the page "Some characteristics of LDPC codes".

Questions

Solution

(1) Correct are the solutions 1 and 3:

With the code word definition $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$, the parity-check matrix $\mathbf{H}_1$ denotes the following check equations:

$$u_1 \oplus u_2 \oplus p_1 = 0\hspace{0.05cm},\hspace{0.3cm} u_3 \oplus u_4 \oplus p_2 = 0\hspace{0.05cm},\hspace{0.3cm} u_1 \oplus u_3 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} u_2 \oplus u_4 \oplus p_4 = 0\hspace{0.05cm}.$$

This corresponds exactly to the assumptions made above. The same result is obtained for $\mathbf{H}_2$ and the code word definition $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.

With the same code word definition $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$ the other parity-check matrices do not yield a meaningful set of equations:

According to parity-check matrix $\mathbf{H}_1$:

$$u_1 \oplus p_1 \oplus u_3 = 0\hspace{0.05cm},\hspace{0.3cm} u_2 \oplus p_2 \oplus p_3 = 0\hspace{0.05cm},\hspace{0.3cm} u_1 \oplus u_2 \oplus u_4 = 0\hspace{0.05cm},\hspace{0.3cm} p_1 \oplus p_2 \oplus p_4 = 0\hspace{0.05cm};$$

corresponding to parity-check matrix $\mathbf{H}_3$:

$$u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} u_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm}u_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} p_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm}u_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm},\hspace{0.15cm} p_1 \hspace{-0.12cm}\oplus\hspace{-0.06cm} u_2 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_3 \hspace{-0.12cm}\oplus\hspace{-0.06cm} p_4 \hspace{-0.05cm} = \hspace{-0.05cm} 0\hspace{0.05cm}.$$

(2) Correct are the proposed solutions 1 and 4:

The code is systematic because $\mathbf{H}_1$ ends with a $4 × 4$ diagonal matrix.
For a regular (LDPC) code, there should be an equal number of ones in each row and in each column.
The first condition is satisfied $(w_{\rm Z} = 3)$, but not the second. Rather, there is (equally often) one one or two ones per column ⇒ ${\rm E}[w_{\rm S}] = 1.5$.
For an irregular code, the lower bound for the code rate is:

$$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} = 1 - \frac{1.5}{3} = 1/2 \hspace{0.05cm}.$$

Because of the given code structure ($k = 4$ information bits, $m = 4$ check bits ⇒ $n = 8$ code bits) the code rate can also be given in the conventional form: $R = k/n$ ⇒ Correct is solution 4 in contrast to answer 3.

(3) The $\mathbf{H}_3$–rows result from linear combinations of $\mathbf{H}_1$–rows:

The first $\mathbf{H}_3$–row is the sum of row 1 and row 4.
The second $\mathbf{H}_3$–row is the sum of row 2 and row 3.
The third $\mathbf{H}_3$–row is the sum of row 1 and row 3.
The fourth $\mathbf{H}_3$–row is the sum of row 2 and row 4.

By linear combinations, the four linearly independent equations with respect to $\mathbf{H}_1$ now become four linearly independent equations with respect to $\mathbf{H}_3$
⇒ Therefore, the proposed solutions 2 and 3 are correct.

(4) Here, solutions 2, 3, and 4 are correct:

If the code described by $\mathbf{H}_3$ were systematic, $\mathbf{H}_3$ should end with a $4 × 4$–diagonal matrix. This is not the case here.
The Hamming weights of all rows are equal $(w_{\rm Z} = 4)$ and also all columns each have the same Hamming weight $(w_{\rm S} = 2)$ ⇒ the code is regular.
This gives $R ≥ 1 - 2/4 = 1/2$ for the code rate. But since the four rows of $\mathbf{H}_3$ also describe four independent equations, the equal sign ⇒ $R = 1/2$ also holds.

	$\mathbf{H}_1$ given $\underline{x} = (u_1, \, u_2, \, u_3, \, u_4, \, p_1, \, p_2, \, p_3, \, p_4)$.
	$\mathbf{H}_1$ given $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.
	$\mathbf{H}_2$ given $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.
	$\mathbf{H}_3$ given $\underline{x} = (u_1, \, p_1, \, u_2, \, p_2, \, u_3, \, p_3, \, u_4, \, p_4)$.

	The code is systematic.
	The code is regular.
	For the code rate holds $R > 1/2$.
	For the code rate holds $R = 1/2$.

	The code is systematic.
	The code is regular.
	For the code rate holds $R ≥ 1/2$.
	For the code rate holds $R = 1/2$.

	No relation between $\mathbf{H}_1$ and $\mathbf{H}_3$ is discernible.
	The $\mathbf{H}_3$ rows are linear combinations of two $\mathbf{H}_1$ rows each.
	The four parity-check equations according to $\mathbf{H}_3$ are linearly independent.