Exercise 4.12: Regular and Irregular Tanner Graph
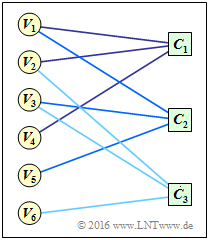
Dargestellt ist ein Tanner–Graph eines Codes $\rm A$ mit
- the variable nodes (abbreviated VNs) $V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ V_6$, where $V_i$ denotes the $i$th code word bit (whether information– or parity bit) and corresponds to the $i$th column of the parity-check matrix;
- the check nodes (abbreviated CNs) $C_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_3$, which represent the rows of the $\mathbf{H}_{\rm A}$ matrix and hence the parity-check equations.
An edge between $V_i$ and $C_j$ indicates that the $i$th code word symbol is involved in the $j$th parity-check equation. In this case, the element $h_{j,\hspace{0.05cm}i}$ of the parity-check matrix is equal $1$.
In the exercise, the relation between the above Tanner–graph $($valid for the code $\rm A)$ and the matrix $\mathbf{H}_{\rm A}$ shall be given. In addition, the Tanner–graph to a parity-check matrix $\mathbf{H}_{\rm B}$ shall be set up, resulting from $\mathbf{H}_{\rm A}$ adding another row. This is to be determined so that the associated code $\rm B$ is regular. This means:
- From all variable nodes $V_i$ $($with $1 ≤ i ≤ n)$ go off equal numbers of edges, likewise from all check nodes $C_j$ $($with $1 ≤ j ≤ m)$.
- The Hamming weights of all rows of $\mathbf{H}_{\rm B}$ are each said to be equal $(w_{\rm Z})$, as are the Hamming–weights of all columns $(w_{\rm S})$.
- For the rate of the regular code to be constructed $\rm B$ the following lower bound then applies:
- $$R \ge 1 - \frac{w_{\rm S}}{w_{\rm Z}} \hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Basics of Low–density Parity–check Codes".
- Reference is made in particular to the page "Two-part LDPC graph representation – Tanner graph".
Questions
Solutiojn
(2) Correct are answers 1 and 3 in contrast to statement 2:
- The second $\mathbf{H}_{\rm A}$–row is rather "$1 \ 0 \ 1 \ 0 \ 1 \ 0$". Thus, this exercise is based on the following parity-check equation:
- $${ \boldsymbol{\rm H}}_{\rm A} = \begin{pmatrix} 1 &1 &0 &1 &0 &0\\ 1 &0 &1 &0 &1 &0\\ 0 &1 &1 &0 &0 &1 \end{pmatrix}\hspace{0.05cm}.$$
- In the diagram, the parity-check equations are illustrated as red (row 1), green (row 2), and blue (row 3) groupings, respectively.
(3) Correct are solutions 1 and 3:
- The $\mathbf{H}$ matrix ends with a $3 × 3$ diagonal matrix ⇒ systematic code.
- Thus, the Hamming weights of the last three columns are $w_{\rm S}(4) = w_{\rm S}(5) = w_{\rm S}(6) = 1$.
- For the first three columns, $w_{\rm S}(1) = w_{\rm S}(2) = w_{\rm S}(3) = 2$ ⇒ irregular code.
- The three matrix rows are linearly independent. Thus $k = n - m = 6 - 3 = 3$ and $R = k/n = 1/2$ holds.
(4) Correct is the proposed solution 1:
- Looking at the previous Tanner–s graph, one can see the correctness of proposed solution 1.
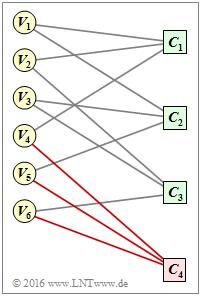
- By adding the row "$0 \ 0 \ 0 \ 1 \ 1 \ 1$" to the $\mathbf{H}_{\rm A}$ matrix, one obtains:
- $${ \boldsymbol{\rm H}}_{\rm B} = \begin{pmatrix} 1 &1 &0 &1 &0 &0\\ 1 &0 &1 &0 &1 &0\\ 0 &1 &1 &0 &0 &1\\ 0 &0 &0 &1 &1 &1 \end{pmatrix}\hspace{0.05cm}.$$
The modifications are marked in red in the adjacent graphic.
Due to the newly added check node $C_4$ and the connections with $V_4, \ V_5$ and $V_6$, there are now
- from all variable nodes $V_i$ two lines, and
- from all Check Nodes $C_j$ uniformly four.
This is the condition for the code $\rm B$ to be regular.
(5) Correct are the solutions 2 and 3:
- The construction in subtask (4) yields a regular code.
- The Hamming weights of the rows and columns, respectively, are $w_{\rm Z} = 3$ and $w_{\rm S} = 2$.
- This gives as lower bound for the code rate:
- $$R \ge 1 - \frac{w_{\rm S}}{w_{\rm Z}} = 1 - {2}/{3} = 1/3 \hspace{0.05cm}.$$
- The $\mathbf{H}$ manipulation does not change the generator matrix $\mathbf{G}$.
- The same code is still sent with code rate $R = 1/2$.