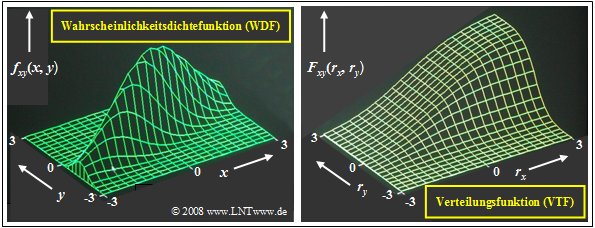
Wahrscheinlichkeitsdichte- und Verteilungsfunktion (1)
Alle bisherigen Aussagen von Kapitel 4 gelten allgemein. Für den Sonderfall Gaußscher Zufallsgrößen – der Name geht auf den Wissenschaftler Carl Friedrich Gauß zurück – können wir weiterhin vermerken:
- Die Verbundwahrscheinlichkeitsdichtefunktion einer Gaußschen 2D-Zufallsgröße $(x, y)$ mit den Mittelwerten $m_x =$ 0 und $m_y =$ 0 sowie dem Korrelationskoeffizienten $ρ_{xy}$ lautet:
$$f_{\rm xy}(x,y)=\frac{\rm 1}{\rm 2\it\pi \sigma_x \sigma_y \sqrt{\rm 1-\rho_{\it xy}^2}}\cdot\exp\Bigg[-\frac{\rm 1}{\rm 2 (1-\it\rho_{xy}^{\rm 2} {\rm)}}\cdot(\frac {\it x^{\rm 2}}{\sigma_x^{\rm 2}}+\frac {\it y^{\rm 2}}{\sigma_y^{\rm 2}}-\rm 2\it\rho_{xy}\cdot\frac{x \cdot y}{\sigma_x \cdot \sigma_y}\rm ) \rm \Bigg].$$
- Ersetzt man in dieser Gleichung $x$ durch $(x – m_x)$ sowie $y$ durch $(y – m_y)$, so ergibt sich die allgemeinere WDF einer zweidimensionalen Gaußschen Zufallsgröße mit Mittelwert.
- Die beiden Randwahrscheinlichkeitsdichtefunktionen $f_{\rm x}(x)$ und $f_{\rm y}(y)$ sind in diesem Fall ebenfalls gaußförmig und weisen die Streuungen $σ_x$ bzw. $σ_y$ auf.
- Bei unkorrelierten Komponenten $x$ und $y$ muss in obiger Gleichung $ρ_{xy} =$ 0 eingesetzt werden, und man erhält dann das Ergebnis:
$$f_{\rm xy}(x,y)=\frac{1}{\sqrt{2\pi}\cdot\sigma_{x}} \cdot\rm e^{-\it {x^{\rm 2}}/{\rm (}{\rm 2\it\sigma_{x}^{\rm 2}} {\rm )}} \cdot\frac{1}{\sqrt{2\pi}\cdot\sigma_{\it y}}\cdot e^{-\it {y^{\rm 2}}/{\rm (}{\rm 2\it\sigma_{y}^{\rm 2}} {\rm )}} = \it f_{\rm x} \rm ( \it x \rm ) \cdot \it f_{\rm y} \rm ( \it y \rm ) .$$
Resümee:
Im Sonderfall einer 2D-Zufallsgröße mit Gaußscher WDF $f_{\rm xy}(x, y)$ folgt aus der Unkorreliertheit auch direkt die statistische Unabhängigkeit: $$f_{\rm xy}(x,y)= f_{\rm x}(x) \cdot f_{\rm y}(y) . $$
Bei keiner anderen WDF kann aus der Unkorreliertheit auf die statistische Unabhängigkeit geschlossen werden. Man kann aber stets ⇒ für jede beliebige 2D–WDF $f_{\rm xy}(x, y)$ von der statistischen Unabhängigkeit auf die Unkorreliertheit schließen, weil:
- Sind zwei Zufallsgrößen $x$ und $y$ völlig voneinander (statistisch) unabhängig, so gibt es zwischen ihnen natürlich auch keine linearen Abhängigkeiten.
Wahrscheinlichkeitsdichte- und Verteilungsfunktion (2)
Das Bild zeigt
- die Wahrscheinlichkeitsdichtefunktion (links) und
- Verteilungsfunktion (rechts)
einer zweidimensionalen Gaußschen Zufallsgröße $(x, y)$ mit relativ starker positiver Korrelation der Einzelkomponenten: $ρ_{xy} =$ 0.8. Wie bei den bisherigen Bildern in diesem Kapitel ist die 2D–Zufallsgröße in $x$–Richtung weiter ausgedehnt als in $y$–Richtung: $σ_x = 2 · σ_y$.
Diese Darstellungen können wie folgt interpretiert werden:
- Die WDF ist vergleichbar mit einem Bergkamm, der sich von links unten nach rechts oben erstreckt.
- Das Maximum liegt bei $m_x =$ 0 und $m_y =$ 0. Das bedeutet, dass die die 2D–Zufallsgröße mittelwertfrei ist.
- Die zweidimensionale VTF als das Integral in zwei Richtungen über die WDF steigt von links unten nach rechts oben von 0 auf 1 kontinuierlich an.
Das nachfolgende Interaktionsmodul erlaubt die Darstellung der zweidimensionalen WDF und der zweidimensionalen VTF für beliebige Werte von $σ_x, σ_y$ und $ρ_{xy}$:
WDF/VTF bei 2D-Gaußgrößen
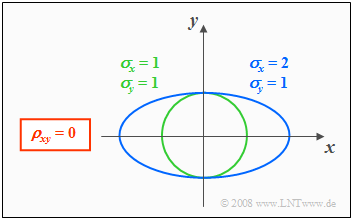
Höhenlinien bei unkorrelierten Zufallsgrößen
Aus der Bedingungsgleichung $f_{\rm xy}(x, y) =$ const. können die Höhenlinien der WDF berechnet werden. Sind die Komponenten $x$ und $y$ unkorreliert $(ρ_{xy} =$ 0), so erhält man:
 $$\frac{x^{\rm 2}}{\sigma_{x}^{\rm 2}}+\frac{y^{\rm 2}}{\sigma_{y}^{\rm 2}} =\rm const.$$
Die Höhenlinien beschreiben in diesem Fall folgende Figuren:
$$\frac{x^{\rm 2}}{\sigma_{x}^{\rm 2}}+\frac{y^{\rm 2}}{\sigma_{y}^{\rm 2}} =\rm const.$$
Die Höhenlinien beschreiben in diesem Fall folgende Figuren:
- Kreise (falls $σ_x = σ_y$, grüne Kurve), oder
- Ellipsen (für $σ_x ≠ σ_y$, blaue Kurve) in Ausrichtung der beiden Achsen.
Weitere Informationen zu dieser Thematik mit Signalbeispielen bietet das folgende Lernvideo: Gaußsche Zufallsgrößen ohne statistische Bindungen (Dauer 2:35).
Sie sehen hier einen Bildschirmabzug dieses Multimedia–Moduls.