AKF am Ausgang eines nichtrekursiven Filters
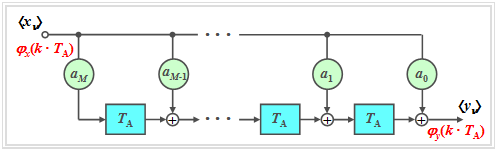
Wir betrachten ein nichtrekursives Laufzeitfilter M-ter Ordnung gemäß der folgenden Grafik. Die zeitdiskrete Eingangsgröße $〈x_ν〉$ ist mittelwertfrei $(m_x =$ 0), gaußverteilt (mit Streuung $σ_x$) und statistisch unabhängig („Weißes Rauschen”).
- Somit gilt für die zeitdiskrete Autokorrelationsfunktion am Eingang:
$$\varphi _x ( {k \cdot T_{\rm A} } ) = \left\{ {\begin{array}{*{20}c} {\sigma _x ^2 } & {\rm{f\ddot{u}r}\quad {\it k} = 0,} \\ 0 & {\rm{f\ddot{u}r}\quad {\it k} \ne 0.} \\\end{array}} \right.$$
- Die AKF der zeitdiskreten Ausgangsfolge $〈y_ν〉$ lautet:
$$\varphi _y ( {k \cdot T_{\rm A} } ) = \sigma _x ^2 \cdot \sum\limits_{\mu = 0}^{M - k} {a_\mu \cdot a_{\mu + k } } \quad {\rm{f\ddot{u}r}}\quad {\it k} = 0, 1,\,...\,,\,{\it M}.$$
- Alle AKF–Werte mit $k > M$ sind 0, und alle AKF–Werte mit $k < M$ sind symmetrisch um 0:
$$\varphi _y ( { - k \cdot T_{\rm A} } ) = \varphi _y ( {k \cdot T_{\rm A} } ).$$
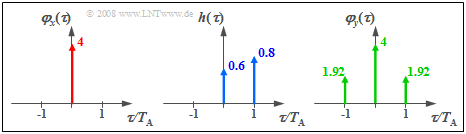
Liegt am Eingang eines nichtrekursiven Filters erster Ordnung (Filterkoeffizienten $a_0 =$ 0.6, $a_1 =$ 0.8) zeitdiskretes weißes Rauschen mit der Streuung $σ_x =$ 2 an, so lauten die diskreten AKF-Werte des Ausgangssignals (alle anderen AKF-Werte sind 0): $$\varphi _y (0) = \sigma _x ^2 \cdot ( {a_0 ^2 + a_1 ^2 }) = 4,\hspace{0.8cm} \varphi _y ( { - T_{\rm A} } ) = \varphi _y ( {T_{\rm A} } ) = \sigma _x ^2 \cdot a_0 \cdot a_1 = 1.92.$$
Die Grafik kann wie fiolgt interpretiert werden:
- Wegen $a_0^2 + a_1^2 =$ 1 besitzt das Ausgangssignal $y(t)$ genau die gleiche Varianz $σ_y^2 = φ_y(0)$ wie das Eingangssignal: $σ_x^2 = φ_x(0) =$ 4.
- Im Gegensatz zur Eingangsfolge $〈x_ν〉$ gibt es bei der Folge $〈y_ν〉$ am Filterausgang statistische Bindungen zwischen benachbarten Abtastwerten.