Exercise 4.2: UMTS Radio Channel Basics

• Return to book

Path loss, frequency– and time–selective fading

UMTS also has quite a few effects leading to degradation that must be taken into account during system planning:

• ${\rm Interference}$:  Since all users are simultaneously served in the same frequency band, each user is interfered by other users.
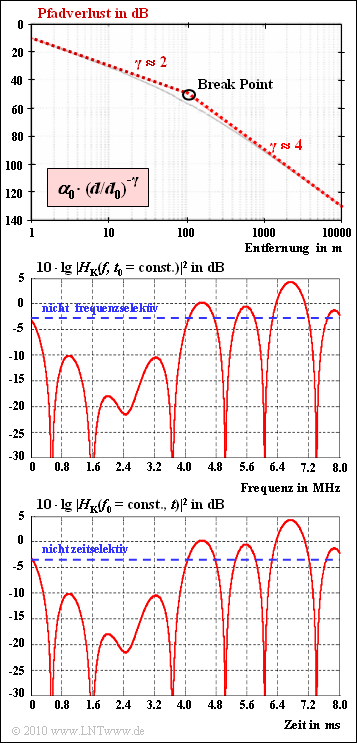
• ${\rm Path\:loss}$:  The received power  $P_{\rm E}$  of a radio signal decreases with distance  $d$  by a factor  $d^{- \gamma}$ .
• ${\rm Multipath\:reception}$:  The signal reaches the mobile receiver not only through the direct path, but through several paths – differently attenuated and differently delayed.
• ${\rm Doppler\:effect}$:  If transmitter and/or receiver move, frequency shifts can occur depending on direction (Which angle? Towards each other? Away from each other?) and speed.

In the book  "Mobile Communications"  these effects have already been discussed in detail. The diagrams convey only a few pieces of information regarding

• Path loss:  Path loss indicates the decrease in received power with distance  $d$  from the transmitter. Above the so-called  break point  applies approximately to the received power:

$$\frac{P(d)}{P(d_0)} = \alpha_0 \cdot \left ( {d}/{d_0}\right )^{-4}.$$

According to the upper graph  $\alpha_{0} = 10^{-5}$  $($correspondingly  $50 \ \rm dB)$  and  $d_{0} = 100 \ \rm m$.

• Frequency-selective fading:  The power transfer function  $|H_{\rm K}(f)|^{2}$  at a given time according to the middle graph illustrates frequency-selective fading. The blue-dashed horizontal line, on the other hand, indicates non-frequency-selective fading.

Such frequency-selective fading occurs when the coherence bandwidth  $B_{\rm K}$  is much smaller than the signal bandwidth  $B_{\rm S}$ . Here, with the  delayspread  $T_{\rm V}$   ⇒   difference between the maximum and minimum delay times:

$$B_{\rm K}\approx \frac{1}{T_{\rm V}}= \frac{1}{\tau_{\rm max}- \tau_{\rm min}}.$$

• Time-selective fading:  The bottom graph shows the power transfer function  $|H_{\rm K}(t)|^{2}$  for a fixed frequency  $f_{0}$. The sketch is to be understood "schematically", because for the time-selective fading considered here exactly the same course was chosen as in the middle diagram for the frequency-selective fading (pure convenience of the author).

Here a so-called Doppler spread  $B_{\rm D}$ arises, defined as the difference between the maximum and the minimum Doppler frequency. The inverse  $T_{\rm D} = 1/B_{\rm D}$  is called  coherence time  or also  correlation duration . In UMTS, time-selective fading occurs whenever  $T_{\rm D} \ll T_{\rm C}$  (chip duration) is.

Hints:

• This exercise belongs to the subject area of  "General Description of UMTS".
• Reference is made in particular to the pages  "Properties of the UMTS radio channel"  and  "Frequency- and time-selective fading".
• For UMTS, the bandwidth is  $B_{\rm S} = 5 \ \rm MHz$  and the chip duration is  $T_{\rm C} \approx 0.26 \ \rm µ s$.

Questions

1

Calculate - starting from the top graph on the information page - the path loss  $($in  $\rm dB)$  for  $d = \rm 5 \ km$.

${\rm path loss} \ = \ $ $\ \rm dB $.

2

What statements are true regarding frequency selective fading?

	This is caused by multipath reception.
	It is caused by movement of transmitter and/or receiver.
	Different frequencies are attenuated differently.
	An echo at a distance  $1\ \rm µ s$  results in frequency selective fading.

3

What statements are true regarding time-selective fading?

	This arises due to multipath reception.
	It results from movement of transmitter and/or receiver.
	Different frequencies are attenuated differently.

Solution

Solution

(1)  According to the sketch, the breakpoint is at $d_{0} = 100 \ \rm m$.

• For $d ≤ d_{0}$, the path loss is equal to $\alpha_{0} \cdot (d/d_{0})^{-2}$. For $d = d_{0} = 100 \ \rm m$ holds:

$${\rm path loss} = \alpha_0 = 10^{-5}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}{50\,{\rm dB}}.$$

• Above $d_{0}$, the path loss is equal to $\alpha_{0} \cdot (d/d_{0})^{-4}$. Thus, at $5 \ \rm km$ distance, one obtains:

$${\rm path loss} = 10^{-5}\cdot 50^{-4} = 1.6 \cdot 10^{-12}\hspace{0.5cm}\rightarrow\hspace{0.5cm}\underline{118\,{\rm dB}}.$$

(2)  Correct statements 1, 3, and 4:

• Frequency selective fading is due to multipath reception. This means:
• Different frequency components are delayed and attenuated differently by the channel.
• This results in attenuation and phase distortion.
• Because $\tau_{\rm max} = 1 \ \rm µ s$ (simplifying $\tau_{\rm min} = 0$ is set) further results in

$$B_{\rm K} = \frac{1}{\tau_{\rm max}- \tau_{\rm min}} = 1\,{\rm MHz}\ \ll \ B_{\rm S} \hspace{0.15cm}\underline {= 5\,{\rm MHz}}.$$

(3)  Correct is statement 2.

• Statements 1 and 3, on the other hand, are valid for frequency-selective fading – see subtask (2).