Gemeinsamkeiten zwischen Phasen– und Frequenzmodulation (1)
Schon im Kapitel 1.3 wurde darauf hingewiesen, dass es zwischen der Phasenmodulation (PM) und der Frequenzmodulation (FM) – siehe Kapitel 3.2 – substanzielle Gemeinsamkeiten gibt. Man fasst deshalb diese beiden verwandten Modulationsverfahren unter dem Oberbegriff „Winkelmodulation” zusammen.
Eine Winkelmodulation – abgekürzt WM – liegt dann vor, wenn sich das modulierte Signal wie folgt darstellen lässt: $$s(t) = A_{\rm T} \cdot \cos(\psi(t)) = A_{\rm T} \cdot \cos( \omega_{\rm T} \cdot t + \phi(t)) \hspace{0.05cm}.$$ Hierbei bezeichnet $A_{\rm T}$ wie bei der Amplitudenmodulation die Amplitude des Trägersignals $z(t)$. Die gesamte Information über das Quellensignal $q(t)$ steckt nun aber in der Winkelfunktion $ψ(t)$.
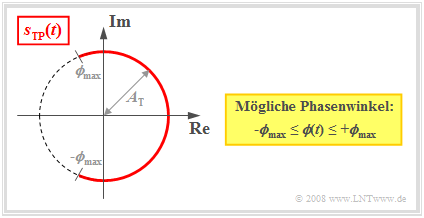
Anhand der Ortskurve – der Darstellung des äquivalenten TP–Signals $s_{\rm TP}(t)$ in der komplexen Ebene – sind folgende Charakteristika der Winkelmodulation zu erkennen (siehe Grafik am Ende des Abschnitts):
- Die Ortskurve ist ein Kreisbogen mit dem Radius $A_{\rm T}$. Daraus folgt, dass die Hüllkurve eines winkelmodulierten Signals stets konstant ist:
$$a(t) = |s_{\rm TP}(t)|= A_{\rm T}= {\rm const.}$$
- Das äquivalente TP–Signal ist bei Winkelmodulation immer komplex und durch eine zeitabhängige Phasenfunktion ${\mathbf ϕ}(t)$ (in Radian) festgelegt, welche die Nulldurchgänge von $s(t)$ bestimmt:
$$s_{\rm TP}(t)= A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t)}\hspace{0.05cm}.$$
- Bei symmetrischem Quellensignal $q(t)$ kann ${\mathbf ϕ}(t)$ alle Werte zwischen $±ϕ_{\rm max}$ annehmen, wobei $ϕ_{\rm max}$ den Phasenhub angibt. Je größer der Phasenhub ist, desto intensiver ist die Modulation.
- Bei einer harmonischen Schwingung ist der Phasenhub $ϕ_{\rm max}$ gleich dem Modulationsindex $η$. Die Verwendung von $η$ zeigt im Folgenden also an, dass $q(t)$ nur eine einzige Frequenz beinhaltet.
- Der Zusammenhang zwischen Quellensignal $q(t)$ und Winkelfunktion $ψ(t) = \cos(ω{\rm T} · t + {\mathbf ϕ}(t))$ bzw. der daraus ableitbaren Phasenfunktion ${\mathbf ϕ}(t)$ unterscheidet sich bei der Phasen– und der Frequenzmodulation grundsätzlich, worauf im Kapitel 3.2 noch ausführlich eingegangen wird.
Gemeinsamkeiten zwischen Phasen– und Frequenzmodulation (2)
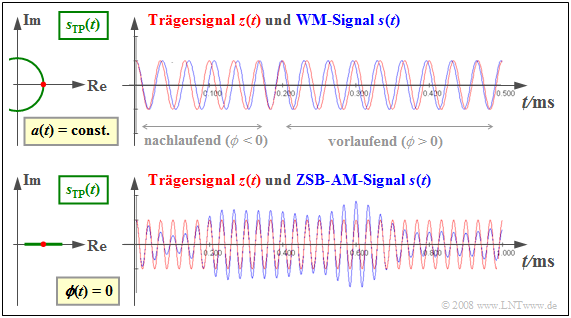
Die folgende Grafik zeigt jeweils rechts das Sendesignal $s(t)$ ⇒ blaue Signalverläufe im Vergleich zum Trägersignal $z(t)$ ⇒ rote Schwingungen sowie links das äquivalente Tiefpass–Signal $s_{\rm TP}(t)$ in der komplexen Ebene. Diese Darstellung in der komplexen Ebene bezeichnen wir auch als die „Ortskurve” ⇒ grüne Kurvenverläufe.
Die obere Skizze gilt für die Winkelmodulation. In diesem Fall beschreibt das äquivalente TP–Signal $s_{\rm TP}(t) = A_{\rm T} · e^{ {\rm j}·ϕ(t)}$ einen Kreisbogen, und es ergibt sich eine konstante Einhüllende $a(t) = A_{\rm T}$.
- Die Information über das Quellensignal $q(t)$ steckt bei der Winkelmodulation ausschließlich in der Lage der Nulldurchgänge von $s(t)$.
- Gilt momentan ${\mathbf ϕ}(t)$ < 0, so treten die Nulldurchgänge von $s(t)$ später auf als diejenigen von $z(t)$. Andernfalls – bei ${\mathbf ϕ}(t)$ > 0 – sind die Nulldurchgänge von $s(t)$ gegenüber $z(t)$ vorlaufend.
Die untere Skizze gilt für die im zweiten Kapitel ausführlich behandelte ZSB–Amplitudenmodulation, gekennzeichnet durch
- die zeitabhängige Hüllkurve $a(t)$ entsprechend dem Quellensignal $q(t)$,
- äquidistante Nulldurchgänge von $s(t)$ gemäß dem Trägersignal $z(t)$, und
- eine horizontale Gerade als Ortskurve $s_{\rm TP}(t)$.
Das Kapitel 3 wurde nach folgenden Gesichtspunkten gegliedert:
- Ein jedes FM–System kann durch einfache Modifikationen in ein entsprechendes PM–System übergeführt werden und umgekehrt.
- Größere Bedeutung bei Analogsystemen hat die FM aufgrund des günstigeren Rauschverhaltens. Deshalb werden Realisierungsaspekte für Modulator/Demodulator erst im Kapitel 3.2 behandelt.
- Die Phasenmodulation ist gegenüber der FM leichter zu verstehen. Deshalb werden zunächst die grundlegenden Eigenschaften eines Winkelmodulationssystems am Beispiel der PM dargelegt.