Discrete Fourier Transform (DFT)

1. Signal Representation
2. Time and Frequency-Discrete Signal Representation
3. Discrete Fourier Transform (DFT)

• Previous page
• Next page

• Previous page
• Next page

Arguments for the discrete implementation of the Fourier transform

The  »Fourier transform«  according to the previous description in chapter  »Aperiodic Signals – Pulses«  has an infinitely high selectivity due to the unlimited extension of the integration interval and is therefore an ideal theoretical tool of spectral analysis.

If the spectral components  $X(f)$  of a time function  $x(t)$  are to be determined numerically,  the general transformation equations

$$\begin{align*}X(f) & = \int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}t\hspace{0.5cm} \Rightarrow\hspace{0.5cm} \text{Transform}\hspace{0.7cm} \Rightarrow\hspace{0.5cm} \text{first Fourier integral} \hspace{0.05cm},\\ x(t) & = \int_{-\infty }^{+\infty}\hspace{-0.15cm}X(f) \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi f t}\hspace{0.1cm} {\rm d}f\hspace{0.35cm} \Rightarrow\hspace{0.5cm} \text{Inverse Transform}\hspace{0.4cm} \Rightarrow\hspace{0.5cm} \text{second Fourier integral} \hspace{0.05cm}\end{align*}$$

are unsuitable for two reasons:

1. The equations apply exclusively to continuous-time signals.  With digital computers or signal processors,  however,  one can only process discrete-time signals.
2. For a numerical evaluation of the two Fourier integrals it is necessary to limit the respective integration interval to a finite value.

$\text{This leads to the following consequence:}$ 

A  »continuous-valued signal«  must undergo two processes before the numerical determination of its spectral properties,  viz.

1. that of  »sampling«  for discretization,  and
   
2. that of  »windowing«  to limit the integration interval.

In the following,  starting from an aperiodic time function  $x(t)$  and the corresponding Fourier spectrum  $X(f)$  a time and frequency-discrete description suitable for computer processing is developed step by step.

Time discretization – Periodification in the frequency domain

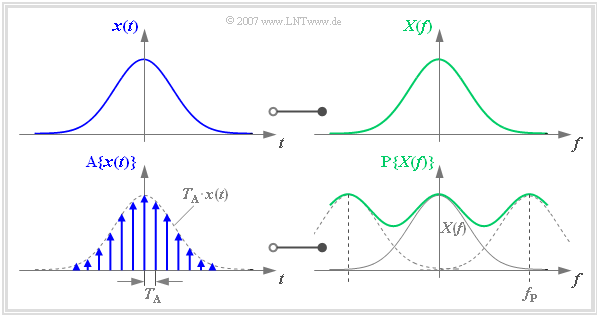
The following graphs show uniformly the time domain on the left and the frequency domain on the right. 

• Without limiting generality,  $x(t)$  and  $X(f)$  are each real and Gaussian.

• According to the chapter  »Discrete-Time Signal Representation«  one can describe the sampling of the time signal  $x(t)$  by multiplying it by a Dirac delta train   ⇒   »Dirac comb  in the time domain«

Time discretization   ⇒   Periodification in the frequency domain.  Notation:
    ${\rm A}\{x(t)\}$:  Signal  $x(t)$  after  »sampling«  $($German:  "Abtastung"$)$   ⇒   $\rm A\{\text{...}\}$
    ${\rm P}\{X(f)\}$:  Spectrum  $X(f)$  after  »periodification«    ⇒   $\rm P\{\text{...}\}$

$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$

The result is the time signal sampled at a distance  $T_{\rm A}$: 

$${\rm A}\{x(t)\} = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$

We transform this sampled signal  $\text{A}\{ x(t)\}$  into the frequency domain:

• The multiplication of the Dirac comb  $p_{\delta}(t)$  with  $x(t)$  corresponds in the frequency domain to the convolution of  $P_{\delta}(f)$  with  $X(f)$.

• The result is the periodified spectrum  $\text{P}\{ X(f)\}$,  where  $f_{\rm P}$  indicates the frequency period of the function  $\text{P}\{ X(f)\}$ :

$${\rm A}\{x(t)\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{X(f)\} = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm P} ).$$

This relation was already derived in the chapter  "Discrete-Time Signal Representation"  but with slightly different nomenclature:

• We now denote the sampled signal by  $\text{A}\{ x(t)\}$  instead of  $x_{\rm A}(t)$.

• The  »frequency period«  is now denoted by  $f_{\rm P} = 1/T_{\rm A}$  instead of  $f_{\rm A} = 1/T_{\rm A}$.

These nomenclature changes are justified in the following sections.

The graph above shows the functional relationship described here.  It should be noted:

1. The frequency period  $f_{\rm P}$  has been deliberately chosen to be small here so that the overlap of the spectra to be summed can be clearly seen.
2. In practice  $f_{\rm P}$  should be at least twice as large as the largest frequency contained in the signal  $x(t)$  due to the sampling theorem.
3. If this is not fulfilled,  then  »aliasing«  must be expected - see chapter  »Possible Errors when using DFT«.

Frequency discretization – Periodification in the time domain

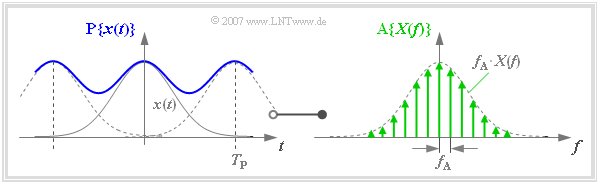
The discretization of  $X(f)$  can also be described by a multiplication with a Dirac comb in the frequency domain.  The result is the sampled spectrum with distance  $f_{\rm A}$:

$${\rm A}\{X(f)\} = X(f) \cdot \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) = \sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot X(\mu \cdot f_{\rm A } ) \cdot\delta (f- \mu \cdot f_{\rm A } )\hspace{0.05cm}.$$

• If one transforms the Dirac comb $($with impulse weights  $f_{\rm A})$  into the time domain,  one obtains with  $T_{\rm P} = 1/f_{\rm A}$:

$$\sum_{\mu = - \infty }^{+\infty} f_{\rm A} \cdot \delta (f- \mu \cdot f_{\rm A } ) \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$

• The multiplication with  $X(f)$  corresponds in the time domain to the convolution with  $x(t)$.  One obtains the signal  $\text{P}\{ x(t)\}$  periodified with distance  $T_{\rm P}$:

$${\rm A}\{X(f)\} \hspace{0.2cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\, \hspace{0.2cm} {\rm P}\{x(t)\} = x(t) \star \sum_{\nu = - \infty }^{+\infty} \delta (t- \nu \cdot T_{\rm P } )= \sum_{\nu = - \infty }^{+\infty} x (t- \nu \cdot T_{\rm P } ) \hspace{0.05cm}.$$

Frequency discretization – Periodization in the time domain

$\text{Example 1:}$  This correlation is illustrated in the graph:

• Due to the coarse frequency rastering,  this example results in a relatively small value for the time period  $T_{\rm P}$ .

• Therefore due to overlaps,  the  $($blue$)$  periodified time signal  $\text{P}\{ x(t)\}$  differs significantly from  $x(t)$.

• If one wants to achieve  $\text{P}\{ x(t)\} \approx x(t)$  then  $T_{\rm P}$  must be chosen much larger than in this example.

Finite signal representation

Finite signals of the Discrete Fourier Transform  $\rm (DFT)$

One arrives at the so-called  »finite signal representation«,  if both

• the time function  $x(t)$, 

• the spectral function  $X(f)$

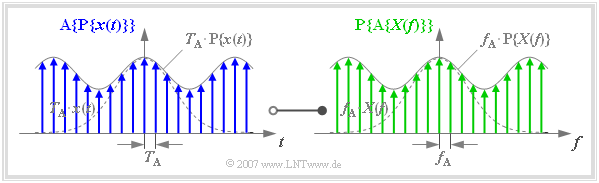
are specified exclusively by their sample values.  This graph is to be interpreted as follows:

• In the left graph,  the function  $\text{A}\{ \text{P}\{ x(t)\}\}$  is drawn in blue.  This results from sampling the periodified time function  $\text{P}\{ x(t)\}$  with equidistant Dirac deltas with distance  $T_{\rm A} = 1/f_{\rm P}$.

• In the right graph,  the function  $\text{P}\{ \text{A}\{ X(f)\}\}$  is drawn in green.  This results from the periodification  $($with  $f_{\rm P})$  of the sampled spectral function  $\{ \text{A}\{ X(f)\}\}$.

• There is a Fourier correspondence between the blue finite signal  $($in the left sketch$)$  and the green finite signal  $($in the right sketch$)$,  as follows:

$${\rm A}\{{\rm P}\{x(t)\}\} \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} \hspace{0.05cm}.$$

• The Dirac delta lines of the periodic continuation  $\text{P}\{ \text{A}\{ X(f)\}\}$  of the sampled spectral function,  however,  only fall into the same frequency grid as those of  $\text{A}\{ X(f)\}$  if the frequency period  $f_{\rm P}$  is an integer multiple  $(N)$  of the frequency sampling interval  $f_{\rm A}$.

• Therefore,  when using the finite signal representation,  the following condition must always be fulfilled,  where in practice the natural number  $N$  is usually a power of two  $($the above graph is based on the value  $N = 8)$:

$$f_{\rm P} = N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {1}/{T_{\rm A}}= N \cdot f_{\rm A} \hspace{0.5cm} \Rightarrow\hspace{0.5cm} N \cdot f_{\rm A}\cdot T_{\rm A} = 1\hspace{0.05cm}.$$

• If the condition  $N \cdot f_{\rm A} \cdot T_{\rm A} = 1$  is fulfilled then the order of periodization and sampling is interchangeable.  Thus:

$${\rm A}\{{\rm P}\{x(t)\}\} = {\rm P}\{{\rm A}\{x(t)\}\}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} {\rm P}\{{\rm A}\{X(f)\}\} = {\rm A}\{{\rm P}\{X(f)\}\}\hspace{0.05cm}.$$

$\text{Conclusions:}$ 

1. The time function  $\text{P}\{ \text{A}\{ x(t)\}\}$  has the period  $T_{\rm P} = N \cdot T_{\rm A}$.
2. The period in the frequency domain is  $f_{\rm P} = N \cdot f_{\rm A}$.
3. For the description of the discretized time and frequency response in each case  $N$  complex numerical values  in the form of impulse weights are sufficient.

$\text{Example 2:}$  A time-limited  $($pulse-like$)$  signal  $x(t)$  is present in sampled form,  where the distance between two samples is  $T_{\rm A} = 1\, {\rm µ s}$:

• After a discrete Fourier transform with  $N = 512$  the spectrum  $X(f)$  is available in form of frequency-samples at spacing  $f_{\rm A} = (N \cdot T_{\rm A})^{-1} \approx 1.953\,\text{kHz}$.

• Increasing the DFT parameter to  $N= 2048$ results in a  $($four times$)$  finer frequency grid with  $f_{\rm A} \approx 488\,\text{Hz}$.

From the continuous to the discrete Fourier transform

From the conventional  »first Fourier integral«

$$X(f) =\int_{-\infty }^{+\infty}x(t) \cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.1cm} {\rm d}t$$

arises from discretization  $(\text{d}t \to T_{\rm A}$,  $t \to \nu \cdot T_{\rm A}$,  $f \to \mu \cdot f_{\rm A}$,  $T_{\rm A} \cdot f_{\rm A} = 1/N)$  the sampled and periodified spectral function

$${\rm P}\{X(\mu \cdot f_{\rm A})\} = T_{\rm A} \cdot \sum_{\nu = 0 }^{N-1} {\rm P}\{x(\nu \cdot T_{\rm A})\}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm} \cdot \hspace{0.05cm}\nu \hspace{0.05cm} \cdot \hspace{0.05cm}\mu /N} \hspace{0.05cm}.$$

It is taken into account that due to the discretization,  the periodified functions are to be used in each case.

For reasons of simplified notation, we now make the following substitutions:

• The  $N$  »time-domain coefficients«  are with the variable  $\nu = 0$, ... , $N - 1$:

$$d(\nu) =. {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.05cm}.$$

• Let  $N$  »frequency domain coefficients«  be associated with the variable  $\mu = 0,$ ... , $N-1$:

$$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big|}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A}}\hspace{0.05cm}.$$

• Abbreviation is written for the from  $N$  dependent  »complex rotation factor« :

$$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} = \cos \left( {2 \pi}/{N}\right)-{\rm j} \cdot \sin \left( {2 \pi}/{N}\right) \hspace{0.05cm}.$$

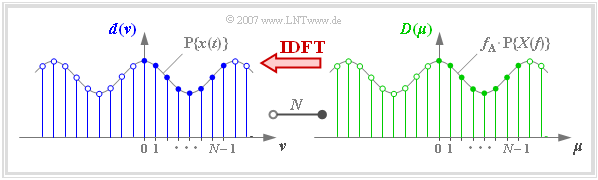
$\text{Definition:}$  The term  »Discrete Fourier Transform«  $\rm (DFT)$  means the calculation of the  $N$  spectral coefficients  $D(\mu)$  from the  $N$  signal coefficients  $d(\nu)$:

On defining the  »Discrete Fourier Transform«  $\rm (DFT)$  with  $N=8$

$$D(\mu) = \frac{1}{N} \cdot \sum_{\nu = 0 }^{N-1} d(\nu)\cdot {w}^{\hspace{0.05cm}\nu \hspace{0.07cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

In the diagram you can see:

• The  $N = 8$  signal coefficients  $d(\nu)$  by the blue filling,

• the  $N = 8$  spectral coefficients  $D(\mu)$  at the green filling.

Inverse discrete Fourier transform

The  »inverse discrete Fourier transform«  describes the  »second Fourier integral«:

$$\begin{align*}x(t) & = \int_{-\infty }^{+\infty}X(f) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm} t}\hspace{0.1cm} {\rm d}f\end{align*}$$

in discretized form:  

$$d(\nu) = {\rm P}\left\{x(t)\right\}{\big|}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A}}\hspace{0.01cm}.$$

$\text{Definition:}$  The term  »Inverse Discrete Fourier Transform»   $\rm (IDFT)$   means the calculation of the signal coefficients  $d(\nu)$  from the spectral coefficients  $D(\mu)$:

On defining the  »Inverse Discrete Fourier Transform«  $\rm (IDFT)$  with  $N=8$

$$d(\nu) = \sum_{\mu = 0 }^{N-1} D(\mu) \cdot {w}^{-\nu \hspace{0.07cm} \cdot \hspace{0.05cm}\mu} \hspace{0.05cm}.$$

• With indices  $\nu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1,$  and   $\mu = 0, \hspace{0.05cm}\text{...} \hspace{0.05cm}, N-1$  holds:

$$d(\nu) = {\rm P}\left\{x(t)\right\}{\big \vert}_{t \hspace{0.05cm}= \hspace{0.05cm}\nu \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm A} }\hspace{0.01cm},$$

$$D(\mu) = f_{\rm A} \cdot {\rm P}\left\{X(f)\right\}{\big \vert}_{f \hspace{0.05cm}= \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}f_{\rm A} } \hspace{0.01cm},$$

$$w = {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi /N} \hspace{0.01cm}.$$

• A comparison between  »DFT«  and  »IDFT«  shows that exactly the same algorithm can be used. 

• The only differences between IDFT and DFT are:

1. The exponent of the rotation factor is to be applied with different sign.
2. In the IDFT,  the division by  $N$  is omitted.

Interpretation of DFT and IDFT

The graph shows the discrete coefficients in the time and frequency domain together with the periodified continuous-time functions.

Time and frequency coefficients of the DFT

When using DFT or IDFT,  please note:

1. According to the above definitions, the DFT coefficients  $d(ν)$  and  $D(\mu)$  always have the unit of the time function.
2. Dividing  $D(\mu)$  by  $f_{\rm A}$,  one obtains the spectral value  $X(\mu \cdot f_{\rm A})$.
3. The spectral coefficients  $D(\mu)$  must always be complex in order to be able to consider odd time functions.
4. One also uses complex time coefficients  $d(\nu)$   ⇒   DFT and IDFT are also applicable to band-pass signals.
5. The basic interval for  $\nu$  and  $\mu$  is usually defined as the range from  $0$  to  $N - 1$  $($filled circles in the graph$)$.

With the complex-valued number sequences 

$$\langle \hspace{0.1cm}d(\nu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}d(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , d(N-1) \hspace{0.1cm}\rangle,$$

$$\langle \hspace{0.1cm}D(\mu)\hspace{0.1cm}\rangle = \langle \hspace{0.1cm}D(0), \hspace{0.05cm}\text{...} \hspace{0.05cm} , D(N-1) \hspace{0.1cm}\rangle,$$

DFT and IDFT are symbolized similarly to the conventional Fourier transform:

$$\langle \hspace{0.1cm} D(\mu)\hspace{0.1cm}\rangle \hspace{0.2cm}\bullet\!\!-\!\!\!-(N)\!-\!\!\!-\!\!\hspace{0.05cm}\circ\, \hspace{0.2cm} \langle \hspace{0.1cm} d(\nu) \hspace{0.1cm}\rangle \hspace{0.05cm}.$$

1. If the function  $x(t)$  is already limited to the range  $0 \le t \lt N \cdot T_{\rm A}$  then the IDFT output directly give the samples of the time function:   $d(\nu) = x(\nu \cdot T_{\rm A}).$
2. If  $x(t)$  is shifted with respect to the basic interval,  one has to choose the association shown in  $\text{Example 3}$  between  $x(t)$  and the coefficients  $d(\nu)$.

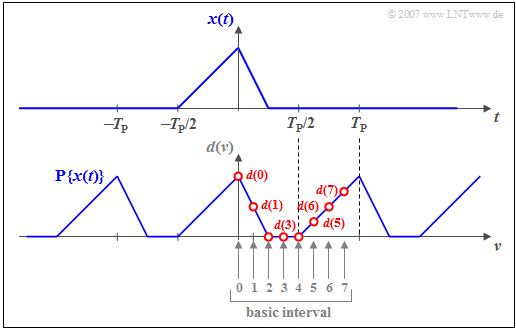
$\text{Example 3:}$  The upper graph shows the asymmetric triangular pulse  $x(t)$ whose absolute width is smaller than  $T_{\rm P} = N \cdot T_{\rm A}$.

On assigning of the DFT coefficients with  $N=8$

The sketch below shows the assigned DFT coefficients $($valid for  $N = 8)$.

• For  $\nu = 0,\hspace{0.05cm}\text{...} \hspace{0.05cm} , N/2 = 4$  holds   $d(\nu) = x(\nu \cdot T_{\rm A})$ :

$$d(0) = x (0)\hspace{0.05cm}, \hspace{0.15cm} d(1) = x (T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(2) = x (2T_{\rm A})\hspace{0.05cm},$$

$$d(3) = x (3T_{\rm A})\hspace{0.05cm}, \hspace{0.15cm} d(4) = x (4T_{\rm A})\hspace{0.05cm}.$$

• The coefficients  $d(5)$,  $d(6)$  and  d$(7)$  are to be set as follows:

$$d(5) = x (-3T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(6) = x (-2T_{\rm A})\hspace{0.05cm}, \hspace{0.35cm} d(7) = x (-T_{\rm A})\hspace{0.05cm}$$

$$\Rightarrow \hspace{0.2cm}d(\nu) = x \big ((\nu\hspace{-0.05cm} - \hspace{-0.05cm} N ) \cdot T_{\rm A}\big ).$$

Exercises for the chapter

Exercise 5.2: Inverse Discrete Fourier Transform

Exercise 5.2Z: DFT of a Triangular Pulse