Allgemeine Beschreibung und Signalraumzuordnung (1)
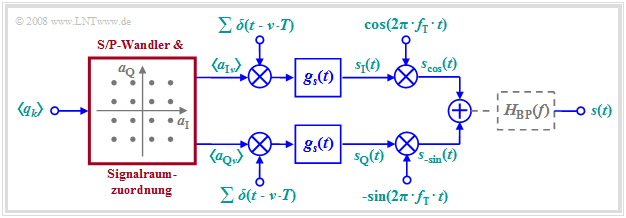
Aufgrund der Orthogonalität von Cosinus und (Minus–)Sinus kann man über einen Übertragungskanal zwei Datenströme unabhängig voneinander übertragen. Die Grafik zeigt das allgemeine Blockschaltbild.
Dieses sehr allgemeine Modell lässt sich wie folgt beschreiben:
- Am Eingang liegt die binäre Quellensymbolfolge $〈q_k〉$ mit der Bitrate $R_{\rm B}$ an. Der zeitliche Abstand zweier Symbole ist damit $T_{\rm B} = 1/R_{\rm B}$.
- Aus jeweils $b$ binären Eingangssymbolen $q_k$ werden zwei mehrstufige Amplitudenkoeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ abgeleitet, wobei „I” für Inphase und „Q” für Quadraturkomponente steht.
- Ist $b$ geradzahlig und die Signalraumzuordnung quadratisch, so können die Koeffizienten $a_{\rm Iν}$ und $a_{\rm Qν}$ jeweils einen von $M = 2^{b/2}$ Amplitudenwerten mit gleicher Wahrscheinlichkeit annehmen. Man spricht dann von Quadratur–Amplitudenmodulation (QAM).
- Das in der Grafik betrachtete Beispiel gilt für die 16–QAM mit $b = M =$ 4 und dementsprechend 16 Signalraumpunkten. Bei einer 256–QAM würde $b =$ 8 und $M =$ 16 gelten $(2^b = M^2 =$ 256).