Aufgaben zu Stochastische Signaltheorie
A1.2 Schaltlogik (D/B-Wandler)
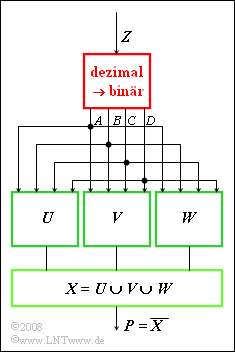
Ein Zahlengenerator $Z$ liefert Dezimalwerte im Bereich von 1 bis 15. Diese werden in Binärzahlen umgewandelt (rot umrandeter Block). Der Ausgang besteht aus den vier Binärwerten $A$, $B$, $C$ und $D$ mit abnehmender Wertigkeit. Beispielsweise liefert $Z = 11$ die Binärwerte $$ A = 1, B = 0, C = 1, D = 1. $$ Mengentheoretisch lässt sich dies wie folgt darstellen: $$ Z = 11\qquad\widehat{=}\qquad A \cap\bar{ B} \cap C \cap D$$ Aus den binären Größen A, B, C und D werden drei weitere Boolsche Ausdrücke gebildet, deren Vereinigungsmenge mit X bezeichnet wird: \[ U = A \cap \bar{D} \] \[ V = \bar{A} \cap B \cap \bar{D} \] $$W, wobei \, \bar{W} = \bar{A} \cup \bar{D} \cup (\bar{B} \cap C) \cup (B \cap \bar{C}). $$ Für die folgenden Fragen ist zu berücksichtigen, dass $Z = 0 ⇒ A = B = C = D = 0$ bereits durch den Zahlengenerator ausgeschlossen ist. Beachten Sie ferner, dass nicht alle Eingangsgrößen $A$, $B$, $C$ und $D$ zur Berechnung aller Zwischengrößen $U$, $V$ und $W$ herangezogen werden. Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 1.2. Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:
Fragebogen zu "A1.2 Schaltlogik (D/B-Wandler)"
Musterlösung zu "A1.1 Musiksignale"
\(f = \frac{10}{20ms} = 500 Hz\) ⇒ Lösungsvorschlag 2.
2. Das Signal \(v_1(t)\) ist gegenüber dem Orginalsignal \(q(t)\) unverzerrt. Es gilt\[v_1(t)=\alpha \cdot q(t-\tau) \]
Eine Dämpfung \(\alpha\) und eine Laufzeit \(\tau\) führen nicht zu Verzerrungen, sondern das Signal ist leiser und es kommt später als das Original ⇒ Lösungsvorschlag 1.
3. Man erkennt sowohl im dargestellten Signalverlauf als auch im Audiosignal das additive Rauschen ⇒ Lösungsvorschläge 1 und 3. Der Signalrauschabstand beträgt dabei ca. 30 dB; dies ist aber aus dieser Darstellung nicht erkennbar.
4. Das Signal \(v_1(t)\) ist formgleich mit dem Originalsignal \(q(t)\) und unterscheidet sich von diesem lediglich durch den Amplitudenfaktor \(\alpha\)=0.3 (entspricht etwa –10 dB) und die Laufzeit \(\tau\)=10 ms.