Exercise 4.6: k-parameters and alpha-parameters
From LNTwww
- Für symmetrische Kupfer–Doppeladern findet man in [PW95] die folgende empirische Formel, gültig für den Frequenzbereich 0 ≤ f ≤ 30 MHz:
- $$\alpha_{\rm I} (f) = k_1 + k_2 \cdot (f/f_0)^{k_3} , \hspace{0.15cm} f_0 = 1\,{\rm MHz} .$$
- Dagegen ist das Dämpfungsmaß eines Koaxialkabels meist in der folgenden Form angegeben:
- $$\alpha_{\rm II}(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}\hspace{0.05cm}.$$
- Insbesondere zur Berechnung von Impulsantwort und Rechteckantwort ist es von Vorteil, auch für die Kupfer–Doppeladern die zweite Darstellungsform mit den Kabelparametern α0, α1 und α2 anstelle der Beschreibung durch k1, k2, und k3 zu wählen. Für die Umrechnung geht man dabei wie folgt vor:
- Aus obigen Gleichungen ist offensichtlich, dass der die Gleichsignaldämpfung charakterisierende Koeffizient k1 gleich α0 ist.
- Zur Bestimmung von α1 und α2 wird davon ausgegangen, dass der mittlere quadratische Fehler im Bereich einer vorgegebenen Bandbreite B minimal sein soll:
- $${\rm E}[\varepsilon^2(f)] = \int\limits_{0}^{ B} \left [ \alpha_{\rm II} (f) - \alpha_{\rm I} (f)\right ]^2 \hspace{0.1cm}{\rm d}f \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{\rm Minimum} \hspace{0.05cm} .$$
- Die Differenz ε2(f) und der mittlere quadratische Fehler E[ε2(f)] ergeben sich dabei wie folgt:
- $$\varepsilon^2(f) \hspace{0.15cm} = \hspace{0.15cm} \left [ \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f} - k_2 \cdot (f/f_0)^{k_3}\right ]^2 =\\ = \hspace{0.15cm}\alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm} f^2 + 2 \alpha_1 \alpha_2 \hspace{0.05cm}\cdot\hspace{0.05cm} f^{1.5} + \alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm} f + k_2^2\hspace{0.05cm}\cdot\hspace{0.05cm} \frac{f^{2k_3}}{f_0^{2k_3}} - 2 k_2 \alpha_1 \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{f^{k_3+1}} {f_0^{k_3}}-{2 k_2 \alpha_2} \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{f^{k_3+0.5}}{f_0^{k_3}}$$
- $$\Rightarrow \hspace{0.3cm}{\rm E}[\varepsilon^2(f)] = \hspace{0.15cm} \alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm}\frac{B^3}{3} + \frac{4}{5} \hspace{0.05cm}\cdot\hspace{0.05cm}\alpha_1 \alpha_2 \hspace{0.05cm}\cdot\hspace{0.05cm}B^{2.5} + \alpha_1^2 \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{B^2}{2} + \frac{k_2^2}{2k_3 +1} \hspace{0.05cm}\cdot\hspace{0.05cm} \frac{B^{2k_3+1}}{f_0^{2k_3}} -\\ - \hspace{0.15cm} \frac{2 k_2 \alpha_1}{k_3 + 2} \hspace{0.05cm}\cdot\hspace{0.05cm} $$
- Diese Gleichung beinhaltet die zu verrechnenden Kabelparameter α1, α2, k2 und k3 sowie die Bandbreite B, innerhalb derer die Approximation gültig sein soll.
- Durch Nullsetzen der Ableitungen von E[ε2(f)] nach α1 bzw. α2 erhält man zwei Gleichungen für die bestmöglichen Koeffizienten α1 und α2, die den mittleren quadratischen Fehler minimieren. Diese lassen sich in folgender Form darstellen:
- $$\frac{{\rm d}\,{\rm E}[\varepsilon^2(f)]}{{\rm d}\,{\alpha_1}} = 0 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \alpha_1 + C_1 \cdot \alpha_2 + C_2 = 0 \hspace{0.05cm} ,\\ \frac{{\rm d}\,{\rm E}[\varepsilon^2(f)]}{{\rm d}\,{\alpha_2}} = 0 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \alpha_1 + D_1 \cdot \alpha_2 + D_2 = 0 \hspace{0.05cm} . $$
- Aus der Gleichung C1 · α2 + C2 = D1 · α2 + D2 lässt sich daraus der Koeffizient α2 berechnen und anschließend aus jeder der beiden oberen Gleichungen der Koeffizient α1.
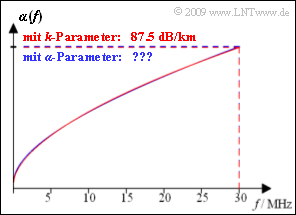
- Die obere Grafik zeigt das Dämpfungsmaß für eine Kupferdoppelader mit 0.5 mm Durchmesser, deren k–Parameter lauten:
- $$k_1 = 4.4\, {\rm dB}/{\rm km} \hspace{0.05cm}, \hspace{0.2cm} k_2 = 10.8\, {\rm dB}/{\rm km}\hspace{0.05cm}, \hspace{0.2cm}k_3 = 0.60\hspace{0.05cm} \hspace{0.05cm}.$$
- Die rote Kurve zeigt die damit berechnete Funktion α(f). Für f = 30 MHz ergibt sich das Dämpfungsmaß α = 87.5 dB/km. Die blaue Kurve gibt die Approximation mit den α–Koeffizienten an. Diese ist von der roten Kurve innerhalb der Zeichengenauigkeit fast nicht zu unterscheiden.
- Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.3.
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.