Voraussetzungen und Optimierungskriterium
Für dieses Kapitel 1.4 gilt das folgende Blockschaltbild:
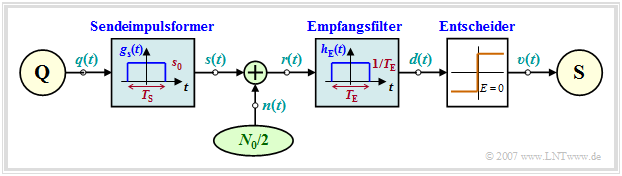
Wenn nicht explizit anders angegeben, wird im Folgenden von folgenden Voraussetzungen ausgegangen:
- Die Übertragung erfolgt binär, bipolar und redundanzfrei; mehrstufige und/oder codierte Systeme werden im Kapitel 2 behandelt. Der Abstand aufeinander folgender Symbole beträgt T. Die (äquivalente) Bitrate ist bei den hier getroffenen Voraussetzungen gleich R = 1/T.
- Der Sendegrundimpuls gs(t) ist rechteckförmig und weist die Amplitude s0 sowie die Impulsdauer TS ≤ T auf. Stimmt die Sendeimpulsdauer TS mit der Symboldauer T überein, so spricht man von NRZ–Rechteckimpulsen. Im Fall TS/T < 1 liegt ein RZ–Format vor.
- Als Übertragungskanal wird das AWGN–Modell mit der (einseitigen) Rauschleistungsdichte N0 verwendet, so dass für das Empfangssignal r(t) = s(t) + n(t) gilt. Die für systemtheoretische Untersuchungen besser geeignete zweiseitige Rauschleistungsdichte beträgt somit N0/2.
- Die Impulsantwort hE(t) des Empfangsfilters ist ebenfalls rechteckförmig, allerdings mit der Höhe 1/TE und der Breite TE. Daraus folgt für den Gleichsignalübertragungsfaktor HE(f = 0) = 1. Nur im Sonderfall TE = TS kann man HE(f) als Matched–Filter bezeichnen.
- Um Impulsinterferenzen auszuschließen, muss bei der Optimierung der beiden Systemparameter TS bzw. TE stets die Randbedingung TS + TE ≤ 2T eingehalten werden. Impulsinterferenzen werden erst im Kapitel 3 Please add link betrachtet.
- Zur Gewinnung der Sinkensymbolfolge wird ein einfacher Schwellenwertentscheider mit optimaler Entscheiderschwelle E = 0 und optimalen Detektionszeitpunkten (bei νT) verwendet.
Unter Systemoptimierung verstehen wir hier, die Parameter TS und TE von Sendegrundimpuls und Empfangsfilter–Impulsantwort so zu bestimmen, dass die Bitfehlerwahrscheinlichkeit den kleinstmöglichen Wert annimmt.