Exercise 3.15: Data Processing Theorem

• Return to book

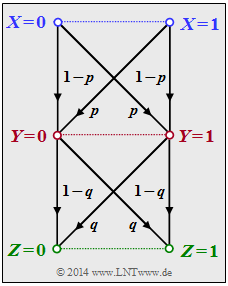
Wir betrachten die folgende Datenverarbeitungskette:

• Binäre Eingangsdaten $X$ werden durch den Prozessor $1$ verarbeitet, der durch bedingte Wahrscheinlichkeiten $(P_Y|X)$ beschreibbar ist. Dessen Ausgangsgröße ist $Y$.
• Ein zweiter Prozessor mit der Zufallsgröße $Y$ am Eingang und der Zufallsgröße $Z$ am Ausgang ist durch $P_{Z|Y} $gegeben. $Z$ hängt allein von $Y$ ab (entweder deterministisch oder stochastisch) und ist unabhängig von $X$:

$$P_{Z\hspace{0.01cm}|\hspace{0.01cm} XY\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} x, y) =P_{Z\hspace{0.01cm}|\hspace{0.01cm} Y\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} y) \hspace{0.05cm}.$$ Hierbei wurde folgende Nomenklatur benutzt: $$x \in X = \{0, 1\}\hspace{0.02cm},\hspace{0.3cm} y \in Y = \{0,1\}\hspace{0.02cm},\hspace{0.3cm} z \in Z = \{0, 1\}\hspace{0.02cm}.$$ Die Verbund–Wahrscheinlichkeitsfunktion (englisch: Joint Probability Mass Function) lautet: $$P_{XYZ}(x, y, z) = P_{X}(x) \cdot P_{Y\hspace{0.01cm}|\hspace{0.01cm} X\hspace{-0.03cm}}(y\hspace{0.01cm}|\hspace{0.01cm} x)\cdot P_{Z\hspace{0.01cm}|\hspace{0.01cm} Y\hspace{-0.03cm}}(z\hspace{0.01cm}|\hspace{0.01cm} y) \hspace{0.05cm}.$$ Das bedeutet auch: $X → Y → Z$ bilden eine Markovkette. Für eine solche gilt das Data Processing Theorem mit folgender Konsequenz: $$I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm}I(X;Y ) \hspace{0.05cm},\\ I(X;Z) \hspace{-0.15cm} \le \hspace{-0.15cm} I(Y;Z ) \hspace{0.05cm}.$$ Das Theorem besagt somit:

• Man kann durch Manipulation (Processing) der Daten $Y$ keine zusätzliche Information über den Eingang $X$ gewinnen.
• Datenverarbeitung (durch den Prozessor 2) dient nur dem Zweck, die Information über $X$ besser sichtbar zu machen.

Hinweis: Die Aufgabe gehört zu Kapitel 3.3.

Fragebogen

1

Wie lässt sich das Ergebnis $I(X; Y) = 1 – H_{bin}(p)$ herleiten?

	Über die Eigenschaften eines streng symmetrischen Kanals.
	Weil $H_{bin}(p)$ eine konkave Funktion ist.
	Das Ergebnis gilt für jede Wahrscheinlichkeitsfunktion $P_X(X).$

2

Welche Transinformation ergibt sich für den Prozessor $1$ mit $p = 0.1$?

$p = 0.1: I(X; Y)$ = $bit$

3

Welche Transinformation ergibt sich für den Prozessor 2 mit $q = 0.2$?

$q = 0.2: I(Y; Z)$ = $bit$

4

Welche Transinformation ergibt sich für das Gesamtsystem?

$p = 0.1, q = 0.2: I(X; Z)$ = $bit$

5

Erfüllt dieses Beispiel das Data Processing Theorem?

	ja
	nein

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.