Das Lerntutorial LNTwww wird vom Lehrstuhls für Nachrichtentechnik (LNT) der Technischen Universität München (TUM) angeboten. Alle Rechte an diesem Tutorial verbleiben bei LNT/TUM und den nachfolgend genannten Autoren.
Weiteres BLABLA
Contents
Signaldarstellung
- Autoren: Günter Söder und Klaus Eichin
- Weitere Beteiligte des LNT:
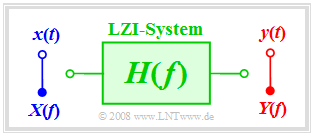
- Mitarbeit von Studenten:Wir betrachten in diesem Kapitel stets das folgende einfache Modell:
Voraussetzungen für die Anwendung der Systemtheorie
Das oben angegebene Modell eines Nachrichtensystems gilt allgemein und unabhängig von den Randbedingungen. Die Anwendung der Systemtheorie erfordert jedoch zusätzlich einige einschränkende Voraussetzungen.
Für das Folgende soll stets gelten, wenn nicht explizit etwas anderes angegeben ist:
- Sowohl $x(t)$ als auch $y(t)$ sind deterministische Signale. Andernfalls muss man entsprechend der Seite Stochastische Systemtheorie im Buch „Stochastische Signaltheorie” vorgehen.
- Das System ist linear. Dies erkennt man zum Beispiel daran, dass eine harmonische Schwingung $x(t)$ am Eingang auch eine harmonische Schwingung $y(t)$ gleicher Frequenz am Ausgang zur Folge hat:
- $$x(t) = A_x \cdot \cos(\omega_0 \hspace{0.05cm}t - \varphi_x)\hspace{0.2cm}\Rightarrow \hspace{0.2cm} y(t) = A_y \cdot\cos(\omega_0 \hspace{0.05cm}t - \varphi_y).$$
- Neue Frequenzen entstehen nicht. Lediglich Amplitude und Phase der harmonischen Schwingung können verändert werden. Nichtlineare Systeme werden im Kapitel Nichtlineare Verzerrungen behandelt.
- Aufgrund der Linearität ist auch das Superpositionsprinzip anwendbar. Dieses besagt, dass aus $x_1(t) ⇒ y_1(t)$ und $x_2(t) ⇒ y_2(t)$ auch zwingend die folgende Zuordnung gilt:
- $$x_1(t) + x_2(t) \hspace{0.1cm}\Rightarrow \hspace{0.1cm} y_1(t) + y_2(t).$$
- Das System ist zeitinvariant. Das bedeutet, dass ein um $\tau$ verschobenes Eingangssignal genau das gleiche Ausgangssignal zur Folge hat – aber ebenfalls um $\tau$ verzögert:
- $$x(t - \tau) \hspace{0.1cm}\Rightarrow \hspace{0.1cm} y(t -\tau)\hspace{0.4cm}{\rm falls} \hspace{0.4cm}x(t )\hspace{0.2cm}\Rightarrow \hspace{0.1cm} y(t).$$
- Zeitvariante Systeme werden im Buch Mobile Kommunikation behandelt.
Sind alle hier aufgeführten Voraussetzungen erfüllt, so spricht man von einem linearen zeitinvarianten System, abgekürzt LZI–System. In der englischsprachigen Literatur ist hierfür die Abkürzung LTI (Linear Time–invariant) gebräuchlich.
Übertragungsfunktion - Frequenzgang
Wir setzen ein LZI–System voraus, dessen Eingangs– und Ausgangsspektrum $X(f)$ bzw. $Y(f)$ bekannt sind oder aus den Zeitsignalen $x(t)$ und $y(t)$ durch Fouriertransformation berechnet werden können.
Das Übertragungsverhalten eines Nachrichtensystems wird im Frequenzbereich durch die Übertragungsfunktion beschrieben: $$H(f) = \frac{Y(f)}{X(f)}= \frac{ {\rm Wirkungsfunktion}}{ {\rm Ursachenfunktion}}.$$ Weitere Bezeichnungen für $H(f)$ sind Systemfunktion und Frequenzgang. Im Folgenden werden wir vorwiegend den letzten Begriff verwenden.
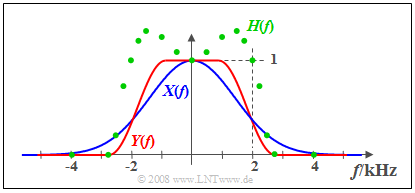
Am Eingang eines LZI–Systems liegt das Signal $x(t)$ mit dem rein reellen Spektrum $X(f)$ an (blaue Kurve). Das gemessene Ausgangsspektrum $Y(f)$ – in der Grafik rot markiert – ist bei Frequenzen kleiner als 2 kHz größer als $X(f)$ und besitzt im Bereich um 2 kHz eine steilere Flanke. Oberhalb von 2.8 kHz hat das Signal $y(t)$ keine Spektralanteile.
Die grünen Kreise markieren einige Messpunkte des ebenfalls reellen Frequenzgangs $H(f)$ = $Y(f)/X(f)$. Bei niedrigen Frequenzen ist $H(f)$ größer als 1, das heißt, in diesem Bereich wirkt das LZI–System verstärkend. Der Flankenabfall von $H(f)$ verläuft ähnlich wie der von $Y(f)$, ist aber nicht identisch mit diesem.
Eigenschaften des Frequenzgangs
Der Frequenzgang $H(f)$ ist eine zentrale Größe bei der Beschreibung nachrichtentechnischer Systeme. Nachfolgend werden einige Eigenschaften dieser wichtigen Systemgröße aufgezählt:
- Der Frequenzgang beschreibt allein das System. Er ist zum Beispiel aus den linearen Bauelementen eines elektrischen Netzwerks berechenbar. Bei anderem Eingangssignal $x(t)$ und dementsprechend anderem Ausgangssignal $y(t)$ ergibt sich der genau gleiche Frequenzgang $H(f)$.
- $H(f)$ kann auch eine Einheit besitzen. Betrachtet man zum Beispiel bei einem Zweipol den Spannungsverlauf $u(t)$ als Ursache und den Strom $i(t)$ als Wirkung, so hat der Frequenzgang $H(f)$ = $I(f)/U(f)$ die Einheit A/V. $I(f)$ und $U(f)$ sind die Fouriertransformierten von $i(t)$ bzw. $u(t)$.
- Im Folgenden betrachten wir ausschließlich Vierpole. Zudem setzen wir ohne Einschränkung der Allgemeingültigkeit meist voraus, dass $x(t)$ und $y(t)$ jeweils Spannungen seien. In diesem Fall ist $H(f)$ stets dimensionslos.
- Da die Spektren $X(f)$ und $Y(f)$ im Allgemeinen komplex sind, ist auch der Frequenzgang $H(f)$ eine komplexe Funktion. Man bezeichnet den Betrag $\\ |H(f)|$ als Amplitudengang. Dieser wird auch oft in logarithmierter Form dargestellt und als Dämpfungsverlauf bezeichnet:
- $$a(f) = - \ln |H(f)| = - 20 \cdot \lg |H(f)|.$$
- Je nachdem, ob die erste Form mit dem natürlichen oder die zweite mit dekadischem Logarithmus verwendet wird, ist die Pseudoeinheit „Neper” (Np) bzw. „Dezibel” (dB) hinzuzufügen.
- Der Phasengang ist aus $H(f)$ in folgender Weise berechenbar:
- $$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in\hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$
- Damit kann der gesamte Frequenzgang auch wie folgt dargestellt werden:
- $$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot\hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
Tiefpass, Hochpass, Bandpass und Bandsperre
Nach dem Amplitudengang $|H(f)|$ unterscheidet man zwischen
- Tiefpass: Signalanteile werden mit zunehmender Frequenz in der Tendenz stärker gedämpft.
- Hochpass: Hier werden hochfrequente Signalanteile weniger gedämpft als niederfrequente. Ein Gleichsignal (also ein Signalanteil mit der Frequenz $f = 0$) kann über einen Hochpass nicht übertragen werden.
- Bandpass: Es gibt eine bevorzugte Frequenz, die man als Mittenfrequenz $f_{\rm M}$ bezeichnet. Je weiter die Frequenz eines Signalanteils von $f_{\rm M}$ entfernt ist, um so stärker wird dieser gedämpft.
- Bandsperre: Dies ist das Gegenstück zum Bandpass und es gilt $|H(f_{\rm M})| ≈ 0$. Sehr niederfrequente und sehr hochfrequente Signalanteile werden dagegen gut durchgelassen.
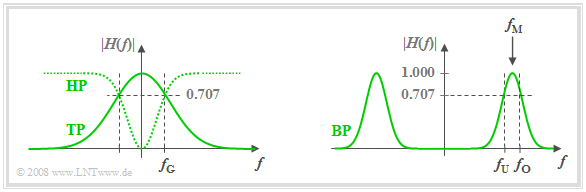
Die Grafik zeigt die Amplitudengänge der Filtertypen TP und HP (links) sowie BP (rechts). Ebenfalls eingezeichnet sind die Grenzfrequenzen $f_{\rm G}$ (bei Tiefpass und Hochpass) bzw. $f_{\rm U}$ und $f_{\rm O}$ (beim Bandpass). Diese bezeichnen hier 3dB–Grenzfrequenzen, zum Beispiel gemäß folgender Definition:
Die 3dB–Grenzfrequenz eines Tiefpasses gibt diejenige Frequenz $f_{\rm G}$ an, für die gilt: $$|H(f = f_{\rm G})| = {1}/{\sqrt{2}} \cdot|H(f = 0)| \hspace{0.5cm}\Rightarrow\hspace{0.5cm} |H(f = f_{\rm G})|^2 = {1}/{2} \cdot|H(f = 0)|^2.$$
Anzumerken ist, dass es für Grenzfrequenzen auch andere Definitionen gibt. Diese finden Sie auf der Seite Allgemeine Bemerkungen
im Kapitel „Einige systemtheoretische Tiefpassfunktionen” .
Testsignale zur Messung von H(f)
Zur messtechnischen Erfassung des Frequenzgangs $H(f)$ eignet sich jedes beliebige Eingangssignal $x(t)$ mit Spektrum $X(f)$, solange $X(f)$ keine Nullstellen aufweist. Durch Messung des Ausgangsspektrums $Y(f)$ lässt sich so der Frequenzgang in einfacher Weise ermitteln: $$H(f) = \frac{Y(f)}{X(f)}.$$ Insbesondere sind folgende Eingangssignale besonders geeignet:
- Diracimpuls $x(t) = K · δ(t)$ ⇒ Spektrum $X(f) = K$:
- Somit ist der Frequenzgang nach Betrag und Phase formgleich mit dem Ausgangsspektrum $Y(f)$ und es gilt $H(f) = 1/K · Y(f)$. Approximiert man den Diracimpuls durch ein schmales Rechteck gleicher Fläche $K$, so muss $H(f)$ mit Hilfe einer ${\rm sin}(x)/x$–Funktion korrigiert werden.
- Diracpuls – die unendliche Summe gleichgewichteter Diracimpulse im zeitlichen Abstand $T_{\rm A}$:
- Dieser führt gemäß Kapitel Zeitdiskrete Signaldarstellung im Buch „Signaldarstellung” zu einem Diracpuls im Frequenzbereich mit Abstand $f_{\rm A} =1/T_{\rm A}$. Damit ist eine frequenzdiskrete Messung von $H(f)$ möglich, mit den spektralen Abtastwerten im Abstand $f_{\rm A}$.
- Harmonische Schwingung $x(t) = A_x · \cos (2πf_0t – φ_x)$ ⇒ diracförmiges Spektrum bei $\pm f_0$:
- Das Ausgangssignal $y(t) = A_y · \cos(2πf_0t – φ_y)$ ist eine Schwingung mit gleicher Frequenz $f_0$. Der Frequenzgang lautet für $f_0 \gt 0$:
- $$H(f_0) = \frac{Y(f_0)}{X(f_0)} = \frac{A_y}{A_x}\cdot{\rm e}^{\hspace{0.05cm} {\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} (\varphi_x - \varphi_y)}.$$ Um den frequenzkontinuierlichen Frequenzgang $H(f)$ zu ermitteln, sind allerdings (unendlich) viele Messungen mit unterschiedlichen Frequenzen $f_0$ erforderlich.
Signaldarstellung
- Autoren: Günter Söder und Klaus Eichin
- Weitere Beteiligte des LNT:
- Mitarbeit von Studenten:
Lineare zeitinvariante Systeme
- Autoren: Günter Söder und Klaus Eichin
- Weitere Beteiligte des LNT:
- Mitarbeit von Studenten:
Inhalt