Contents
Signalraumdarstellung der linearen Modulation (1)
Im bisherigen Kapitel 4 wurde die Struktur des optimalen Empfängers und die Signaldarstellung mittels Basisfunktionen am Beispiel der Basisbandübertragung behandelt. Mit der gleichen Systematik und der gleichen Einheitlichkeit sollen nun auch Bandpass–Systeme betrachtet werden, die bereits in früheren Büchern bzw. Kapiteln beschrieben wurden, nämlich
- im Kapitel 4 des Buches „Modulationsverfahren”,
- im Kapitel 1.5 des vorliegenden Buches.
Dabei beschränken wir uns im Kapitel 4.4 auf
- lineare Modulationsverfahren, und
- kohärente Demodulation
Das bedeutet, dass am Empfänger das beim Sender zugesetzte Trägersignal hinsichtlich Frequenz und Phase exakt bekannt sein muss.
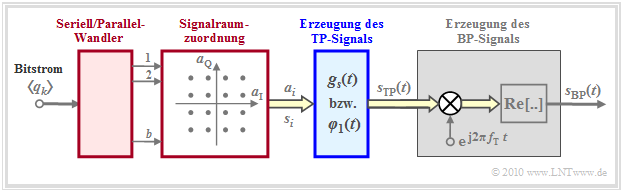
In diesem Fall kann das gesamte Übertragungssystem im äquivalenten Tiefpassbereich beschrieben werden und der Zusammenhang zur Basisbandübertragung ist noch offensichtlicher zu erkennen als bei Betrachtung der Bandpass–Signale. Es ergibt sich somit das folgende Modell, das auf der nächsten Seite im Detail beschrieben wird.
Die Beschreibung der nichtlinearen Modulationsverfahren und der nichtkohärenten Demodulation folgt im Kapitel 4.5.
Signalraumdarstellung der linearen Modulation (2)
Zum Übertragungsmodell der letzten Seite ist Folgendes zu bemerken:
- Aus dem ankommenden Bitstrom 〈qk〉 ∈ {0, L} werden je b Datenbits seriell/parallel gewandelt. Diese Ausgangsbits ergeben die Nachricht m ∈ {m0, ..., mM–1}, wobei M = 2b die Stufenzahl angibt. Für das Folgende wird die Nachricht m = mi vorausgesetzt.
- In der Signalraumzuordnung wird jeder Nachricht mi ein komplexer Amplitudenkoeffizient <nobr>ai = aIi + j · aQi</nobr> zugeordnet, dessen Realteil die Inphasekomponente und dessen Imaginärteil die Quadraturkomponente des späteren Sendesignals formen wird.
- Am Ausgang des blau markierten Blockes Erzeugung des TP–Signals liegt das (im allgemeinen) komplexwertige Tiefpass–Signal
- \[s_{\rm TP}(t) \big {|}_{m \hspace{0.05cm}= \hspace{0.05cm} m_i} = a_i \cdot g_s(t) = a_{{\rm I}i} \cdot g_s(t) + {\rm j} \cdot a_{{\rm Q}i} \cdot g_s(t)\]
- vor, wobei gs(t) vorerst ebenso wie sTP(t) auf den Bereich 0 ≤ t < T beschränkt sein soll und der Index i wiederum einen Hinweis auf die gesendete Nachricht mi liefert.
- Durch Energienormierung kommt man vom Sendegrundimpuls gs(t) zur Basisfunktion
- \[\varphi_1(t) = { g_s(t)}/{\sqrt{E_{gs}}} \hspace{0.4cm} {\rm mit} \hspace{0.4cm} E_{gs} = \int_{0}^{T} g_s(t)^2 \,{\rm d} t \]
- \[\Rightarrow \hspace{0.3cm} s_{\rm TP}(t) \big {|}_{m\hspace{0.05cm} =\hspace{0.05cm} m_i} = s_{{\rm I}i} \cdot \varphi_1(t) + s_{{\rm Q}i} \cdot {\rm j} \cdot \varphi_1(t) \hspace{0.05cm}.\]
- Während die Koeffizienten aIi und aQi dimensionslos sind, weisen die neuen Koeffizienten sIi und sQi die Einheit „Wurzel aus Energie” auf – siehe auch Kapitel 4.1:
- \[s_{{\rm I}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm I}i}\hspace{0.05cm}, \hspace{0.2cm} s_{{\rm Q}i} = {\sqrt{E_{gs}}} \cdot a_{{\rm Q}i}\hspace{0.05cm}. \]
- Die obere Gleichung zeigt weiter, dass das hier betrachtete System im äquivalenten TP–Bereich durch je eine reelle Basisfunktion φ1(t) und eine rein imaginäre Basisfunktion ψ1(t) = j · φ1(t) oder durch eine einzige komplexe Basisfunktion ξ1(t) vollständig beschrieben wird.
- Der grau hinterlegte Teil des Blockschaltbildes zeigt das Modell zur Erzeugung des BP–Signals sBP(t), zuerst die Multiplikation des TP–Signals sTP(t) mit dem komplexen Drehzeiger exp(j2πfTt) – auf diese Weise ergibt sich das analytische Signal s+(t) – und anschließend die Realteilbildung.
- Die beiden Basisfunktionen des Bandpass–Signals sBP(t) ergeben sich hier als energienormierte und auf den Bereich 0 ≤ t ≤ T zeitbegrenzte Cosinus– bzw. Minus–Sinus–Schwingungen.
Im Folgenden beschränken wir uns aber auf die Darstellung des äquivalenten Tiefpass–Signals sTP(t).
Hinweis: Im skizzierten Modell sind komplexe Größen durch einen gelb gefüllten Doppelpfeil markiert. Diese Vereinbarung soll auch für alle nachfolgenden Grafiken gelten.