Fehlerkorrelationsfunktion des BSC–Modells
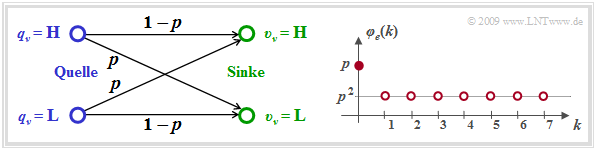
Die linke Grafik zeigt mit dem BSC–Modell das einfachste Modell eines digitalen Übertragungssystems.
Der Name steht für Binary Symmetric Channel und besagt, dass dieses Modell nur bei Binärsystemen mit symmetrischen Verfälschungseigenschaften angewendet werden kann. Weiter gilt:
- Das BSC–Modell eignet sich für die Untersuchung und Erzeugung einer Fehlerfolge mit statistisch unabhängigen Fehlern. Man nennt einen solchen Kanal auch gedächtnisfrei und es existiert nur ein einziger Kanalzustand.
- Die beiden Symbole (zum Beispiel L und H) werden jeweils mit der gleichen Wahrscheinlichkeit p verfälscht, so dass auch die mittlere Fehlerwahrscheinlichkeit pM gleich p ist, und zwar unabhängig von den Symbolwahrscheinlichkeiten pL und pH.
Die rechte Grafik zeigt die Fehlerkorrelationsfunktion (FKF)
\[\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] = \left\{ \begin{array}{c} p \\ p^2 \end{array} \right.\quad \begin{array}{*{1}c} f{\rm \ddot{u}r }\hspace{0.25cm}k = 0 \hspace{0.05cm}, \\ f{\rm \ddot{u}r }\hspace{0.25cm} k > 0 \hspace{0.05cm}.\\ \end{array}\]
Bitte beachten Sie:
- Beim BSC–Modell wird also der FKF–Endwert (Quadrat der mittleren Fehlerwahrscheinlichkeit), der bei anderen Modellen erst für k → ∞ gültig ist, bereits bei k = 1 exakt erreicht.
- Das BSC–Modell gehört zur Klasse der erneuernden Kanalmodelle (Renewal Channels). Bei einem erneuernden Kanalmodell sind die Fehlerabstände statistisch voneinander unabhängig und die Fehlerkorrelationsfunktion kann in einfacher Weise iterativ berechnet werden:
- \[\varphi_{e}(k) = \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa) \cdot \varphi_{e}(k - \kappa) \hspace{0.05cm}.\]