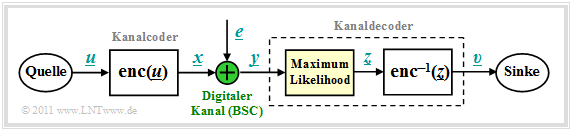
Blockschaltbild und Voraussetzungen
Wir gehen von dem bereits im Kapitel 1.2 gezeigten Blockschaltbild aus, wobei als Kanalmodell meist der Binary Symmetric Channel (BSC) verwendet wird. Zur Codewortschätzung verwenden wir den Maximum–Likelihood–Entscheider (ML), der für binäre Codes ⇒ x ∈ GF(2n) das gleiche Ergebnis liefert wie der MAP–Empfänger.
Die Aufgabe des Kanaldecoders kann wie folgt beschrieben werden:
- Der Vektor υ nach der Decodierung (an der Sinke) soll möglichst gut mit dem Informationswort u übereinstimmen. Das heißt: Die Blockfehlerwahrscheinlichkeit soll möglichst klein sein:
- \[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
- Aufgrund der deterministischen Zuweisungen x = enc(u) bzw. υ = enc–1(z) gilt aber auch:
- \[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{z} \ne \underline{x}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
- Gesucht ist somit das zum gegebenen Empfangswort y = x + e am wahrscheinlichsten gesendete Codewort xi, das als Ergebnis z weiter gegeben wird:
- \[\underline{z} = {\rm arg} \max_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} {\rm Pr}( \underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm}|\hspace{0.05cm} \underline{y} ) \hspace{0.05cm}.\]
- Beim BSC–Kanal gilt sowohl xi ∈ GF(2n) als auch y ∈ GF(2n), so dass die ML–Regel auch mit der Hamming–Distanz dH(y, xi) geschrieben werden kann:
- \[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{x}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]