Exercise 1.2: Signal Classification

Aufgabe zu Klassifizierung von Signalen

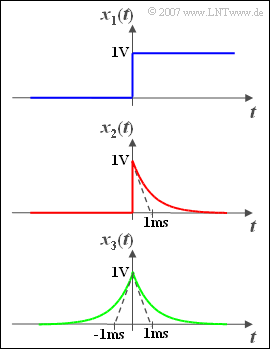
Nebenstehend sind drei Signalverläufe dargestellt:

Das Signal $x_1(t)$ wird genau zum Zeitpunkt $t = 0$ eingeschaltet und besitzt für $t > 0$ den Wert $1\,\text{V}$.
Das rote Signal $x_2(t)$ ist für $t < 0$ identisch $0$, springt bei $t = 0$ auf $1\,\text{V}$ an und fällt danach mit der Zeitkonstanten $1\,\text{ms}$ ab. Für $t > 0$ gilt:

\[x_2(t) = 1\,\text{V} \cdot {\rm e}^{- {t}/(1\,\text{ms})}.\]

Entsprechend gilt für das grün dargestellte Signal für alle Zeiten $t$:

\[x_3(t) = 1\,\text{V} \cdot {\rm e}^{- {|t|}/(1\,\text{ms})}.\]

Diese drei Signale sollen nun von Ihnen nach den folgenden Kriterien klassifiziert werden:

deterministisch bzw. stochastisch,
kausal bzw. akausal,
energiebegrenzt bzw. leistungsbegrenzt,
wertkontinuierlich bzw. wertdiskret,
zeitkontinuierlich bzw. zeitdiskret.

Hinweis: Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen zu „Aufgabe 1.2: Signalklassifizierung”

Musterlösung zu "A1.1 Musiksignale"

Solution

1. Alle Signale können in analytischer Form vollständig beschrieben werden; sie sind deshalb auch deterministisch. Alle Signale sind außerdem für alle Zeiten $t$ eindeutig definiert, nicht nur zu gewissen Zeitpunkten. Deshalb handelt es sich stets um zeitkontinuierliche Signale.

Die Signalamplituden von $x_2(t)$ und $x_3(t)$ können alle beliebigen Werte zwischen $0$ und $1\,\text{V}$ annehmen; sie sind deshalb wertkontinuierlich.

Dagegen sind beim Signal $x_1(t)$ nur die zwei Signalwerte $0$ und $1\,\text{V}$ möglich, und es liegt ein wertdiskretes Signal vor. Zutreffend sind also die Lösungsvorschläge 1 und 3.

2. Ein Signal bezeichnet man als kausal, wenn es für Zeiten $t < 0$ nicht existiert bzw. identisch $0$ ist. Dies gilt für die beiden ersten Signale $x_1(t)$ und $x_2(t)$. Dagegen gehört $x_3(t)$ zur Klasse der akausalen Signale.

3. Nach der allgemeinen Definition gilt\[E_2 = \lim_{T_M \to \infty}\int_{-{T_M}/{2}}^{{T_M}/{2}} x_2^{2}(t)dt\]

Im vorliegenden Fall ist die untere Integrationsgrenze 0 und es kann auf die Grenzwertbildung verzichtet werden. Man erhält\[E_2 = \int_{0}^{\infty}(1V)^{2} \cdot e^{-\frac{2t}{1ms}} dt = 5 \cdot 10^{-4} V^{2}s \]

Bei endlicher Energie ist die zugehörige Leistung stets verschwindend klein. Daraus folgt P2 = 0.

4. Wie bereits unter Punkt 3. berechnet wurde, besitzt $x_2(t)$ eine endliche Energie\[E_2 = 5 \cdot 10^{-4} V^2s\].

Die Energie des Signals $x_3(t)$ ist doppelt so groß, da nun der Zeitbereich t < 0 den gleichen Beitrag liefert wie der Zeitbereich t > 0. Also ist

$E_3 = 10^{-3} V^2s$

⇒ Richtig sind die Lösungsvorschläge 2 und 3.

Beim Signal $x_1(t)$ divergiert das Energieintegral\[E_1 \rightarrow \infty\].

Dieses Signal weist eine endliche Leistung auf

$P_1 = 0.5 V^2$

und ist dementsprechend leistungsbegrenzt. Das Ergebnis berücksichtigt, dass das Signal in der Hälfte der Zeit ($t < 0$) identisch $0$ ist.

	Alle hier betrachteten Signale sind deterministisch.
	Alle hier betrachteten Signale sind von stochastischer Natur.
	Es handelt sich stets um zeitkontinuierliche Signale.
	Es handelt sich stets um wertkontinuierliche Signale.

	\(x_1(t)\)
	\(x_2(t)\)
	\(x_3(t)\)

	\(x_1(t)\)
	\(x_2(t)\)
	\(x_3(t)\)