Contents
- 1 Blockschaltbild und Voraussetzungen zu Kapitel 2.5
- 2 Mögliche Codewortschätzer: HD–MLD bzw. BDD (1)
- 3 Mögliche Codewortschätzer: HD–MLD bzw. BDD (2)
- 4 Vorgehensweise beim „Bounded Distance Decoding”
- 5 Schritt (A): Auswertung des Syndroms beim BDD
- 6 Error Locator Polynom – Definition und Eigenschaften (1)
- 7 Error Locator Polynom – Definition und Eigenschaften (2)
- 8 Schritt (B): Aufstellen/Auswerten des ELP–Koeffizientenvektors (1)
- 9 Schritt (B): Aufstellen/Auswerten des ELP–Koeffizientenvektors (2)
- 10 Schritt (C): Lokalisierung der Fehlerstellen
- 11 Schritt (D): Abschließende Fehlerkorrektur
- 12 Schnelle Reed–Solomon–Decodierung
- 13 Aufgaben
- 14 Quellenverzeichnis
Blockschaltbild und Voraussetzungen zu Kapitel 2.5
Wie im Kapitel 2.4 betrachten wir ein Übertragungssystem mit Reed–Solomon–Codierung, das durch die beiden Codeparameter n = 2m – 1 und k gekennzeichnet ist. Mit der Generatormatrix G lautet der Zusammenhang zwischen dem Informationswort u und dem Codewort c:
\[\underline {c} = {\rm enc}(\underline {u}) = \underline {u} \cdot { \boldsymbol{\rm G}} \hspace{0.3cm} {\rm mit} \hspace{0.3cm}\underline {u} = (u_0, u_1, ... \hspace{0.05cm}, u_i, ...\hspace{0.05cm}, u_{k-1})\hspace{0.05cm}, \hspace{0.2cm} \underline {c} = (c_0, c_1, ... \hspace{0.05cm}, c_i, ...\hspace{0.05cm}, c_{n-1}) \hspace{0.05cm}.\]
Sowohl die Informationssymbole ui als auch die Codesymbole ci entstammen dem Körper GF(q) mit q = n + 1 = 2m, und sind somit durch m Binärsymbole (Bit) darstellbar.
Ein Vergleich dieses Blockschaltbildes mit dem entsprechenden Modell zu Kapitel 2.4 zeigt:
- Der wesentliche Unterschied liegt im verwendeten diskreten Kanalmodell (grün hinterlegt). Anstelle des Auslöschungskanals („m–BEC”) wird nun der m–BSC betrachtet. Für jedes einzelne Bit des Codesymbols ci wird der Binary Symmetric Channel (BSC) angewandt. Ist auch nur ein Bit innerhalb des Codesymbols verfälscht, so ist yi ≠ ci.
- Im Kapitel 2.4 sind unsichere Bit bereits durch Auslöschungen E (Erasures) markiert. Aufgabe des Codewortfinders (CWF) ist es deshalb, aus dem verstümmelten Empfangswort y das Decodierergebnis z zu rekonstruieren. Ist die Anzahl e der Auslöschungen kleiner als die minimale Distanz dmin, so gelingt dies und man erhält z = c. Andernfalls meldet der CWF, dass er das aktuelle Empfangswort y nicht decodieren kann. Eine Fehlentscheidung (z ≠ c) ist ausgeschlossen.
- In diesem Kapitel wird nun der erste Decoderblock als Codewortschätzer (CWS) bezeichnet. Die Namensgebung soll deutlich machen, dass aufgrund des m–BSC–Modells Fehlentscheidungen (z ≠ c) unvermeidlich sind, nämlich dann, wenn durch mehrere Symbolfehler das Empfangswort y zu einem gültigen Codewort verfälscht wurde.
Aufgabe des Decoders ist es, seinen Ausgangsvektor υ so zu bestimmen, dass er „möglichst gut” mit dem Informationswort u übereinstimmt. Oder etwas genauer formuliert:
\[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{\upsilon} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
Aufgrund des deterministischen Mappings c = enc(u) und υ = enc–1(z) gilt in gleicher Weise:
\[{ \rm Pr(Blockfehler)} = { \rm Pr}( \underline{z} \ne \underline{c}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]
Deshalb werden im Folgenden die zwei gelb hinterlegten Blöcke nicht weiter betrachtet. Im Mittelpunkt der Betrachtungen steht vielmehr der rot hinterlegte Codewortschätzer (CWS).
Mögliche Codewortschätzer: HD–MLD bzw. BDD (1)
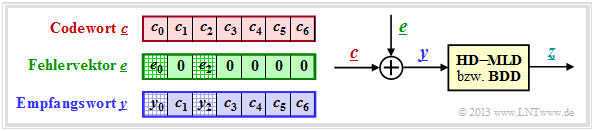
Die rechte Skizze der nachfolgenden Grafik verdeutlicht nochmals die Aufgabenstellung, wobei hier das Kanalmodell „m–BSC” durch den additiven Fehlervektor e = y – c ersetzt ist. Die linke Skizze verdeutlicht den Zusammenhang zwischen diesen drei Vektoren.
Diese Aufgabenstellung soll durch ein Beispiel verdeutlicht werden.
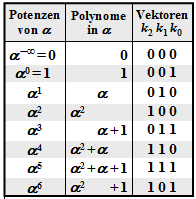
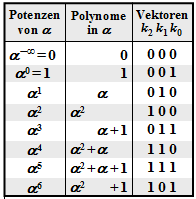
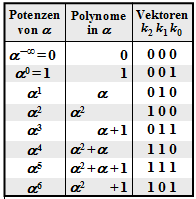
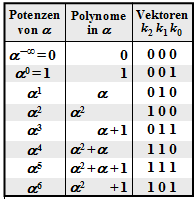
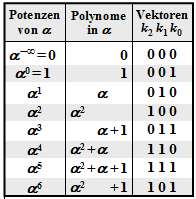
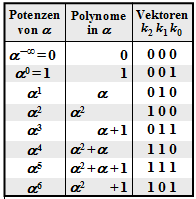 Alle nachfolgend genannten Symbole sind Elemente von GF(23) = {0, 1, α1, α2, α3, α4, α5, α6}. Zur Umrechnung zwischen der Koeffizientendarstellung (mit der Reihenfolge k2, k1, k0) und der Exponentendarstellung (als Potenzen des primitiven Elements α) kann die nebenstehende Tabelle verwendet werden.
Alle nachfolgend genannten Symbole sind Elemente von GF(23) = {0, 1, α1, α2, α3, α4, α5, α6}. Zur Umrechnung zwischen der Koeffizientendarstellung (mit der Reihenfolge k2, k1, k0) und der Exponentendarstellung (als Potenzen des primitiven Elements α) kann die nebenstehende Tabelle verwendet werden.
Codewort und Empfangswort lauten in Koeffizientendarstellung:
\[\underline{c} \hspace{-0.15cm} = \hspace{-0.15cm} \Big ( (010), (001), (100),(010),(100),(111),(111)\Big )\hspace{0.05cm},\] \[\underline{y} \hspace{-0.15cm} = \hspace{-0.15cm} \Big ( (011), (001), (000),(010),(100),(111),(111)\Big )\hspace{0.05cm}.\]
Damit ergibt sich für den Fehlervektor e = y – c:
\[\underline{e} \hspace{0.05cm} = \hspace{0.05cm} \Big ( (001), (000), (100), (000),(000),(000),(000)\Big )\hspace{0.05cm}.\]
Umgewandelt in die Exponentendarstellung erhält man:
\[\underline{c} \hspace{-0.15cm} = \hspace{-0.15cm} \Big ( \alpha^1, 1, \alpha^2,\alpha^1,\alpha^2,\alpha^5,\alpha^5\Big )\hspace{0.05cm},\]
\[\underline{y} \hspace{-0.15cm} = \hspace{-0.15cm} \Big ( \alpha^3, 1, \hspace{0.09cm}0\hspace{0.09cm},\alpha^1,\alpha^2,\alpha^5,\alpha^5\Big ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline{e} = \Big ( \hspace{0.05cm}1, \hspace{0.05cm}0, \hspace{0.05cm}\alpha^2,\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}0,\hspace{0.05cm}0\hspace{0.05cm}\Big )\hspace{0.05cm}.\]
Aufgabe des Codewortschätzers (CWS) ist es, das zu y wahrscheinlichste Codewort ci zu finden und sein Ergebnis z = ci an das nachfolgende Mapping weiterzugeben. Es gibt verschiedene Möglichkeiten:
- Hard Decision Maximum Likelihood Decoding (HD–MLD),
- Bounded Distance Decoding (BDD),
- Decodierung über die halbe Mindestdistanz.
Diese Decodierprinzipien werden auf der nächsten Seite ausführlicher behandelt.
Mögliche Codewortschätzer: HD–MLD bzw. BDD (2)
Aufgabe des Codewortschätzers (CWS) ist es, das zu y wahrscheinlichste Codewort ci zu finden und sein Ergebnis z = ci weiterzugeben. Hierfür gibt es mehrere Möglichkeiten:
Hard Decision Maximum Likelihood Decoding (HD–MLD):
Man wählt von allen möglichen Reed–Solomon–Codeworten ci (hiervon gibt es insgesamt qk) dasjenige mit der geringsten Hamming–Distanz zum Empfangswort y aus. Somit lautet das Ergebnis:
\[\underline{z} = {\rm arg} \min_{\underline{x}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}_{\rm RS}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{c}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]
Die Entscheidung passiert hier auf der maximalen Rückschlusswahrscheinlichkeit Pr(ci | y) und führt zum bestmöglichen Ergebnis. Näheres siehe Kapitel 1.2. Es wird stets entschieden, selbst wenn die Anzahl r der Symbolfehler größer ist als die Korrekturfähigkeit t des Codes. In einem solchen Fall ist allerdings das Decodierergebnis sehr unsicher.
Es sei nochmals erwähnt, dass bei ML–Decodierung immer entschieden wird. Ein Decodierversagen ist ausgeschlossen. Aber natürlich gibt es auch falsche Entscheidungen.
Bounded Distance Decoding (BDD):
Falls die Anzahl r der Symbolfehler im Empfangswort y nicht größer ist als die Korrekturfähigkeit t = ⌊(dmin – 1)/2⌋ des Codes, kann man die r Symbolfehler vollständig korrigieren. Der Fall r > t führt zu einem Abbruch des Decodiervorgangs ohne Ergebnis. Anders ausgedrückt: Es werden nur diejenigen Empfangsworte zum Kugelmittelpunkt decodiert, die in einer Kugel um diesen mit Radius t liegen. Andere werden als undecodierbar markiert, zum Beispiel als Erasure.
Decodierung über die halbe Mindestdistanz:
Hier wird auch im Fall r > t versucht, das Codewort zu decodieren. Im Gegensatz zu HD–MLD, das ebenfalls über die halbe Mindestdistanz hinaus decodiert, ist hier aber ein Decodierversagen nicht per se ausgeschlossen.
Für den Rest dieses Kapitels beschäftigen wir uns ausschließlich mit Bounded Distance Decoding. Der Grund hierfür ist die enorme Komplexität der Maximum Likelihood Detection proportional zu qn–k.
Vorgehensweise beim „Bounded Distance Decoding”
Im Folgenden werden die einzelnen Schritte des BDD–Algorithmuses kurz und rezeptartig beschrieben. Auf den nächsten Seiten werden dann die einzelnen Punkte genauer behandelt und die Vorgehensweise an typischen Beispielen verdeutlicht.
(A) Berechne das Syndrom s = y · HT:
- Ergibt sich aus dem Empfangswort y und der Prüfmatrix H des Codes das Syndrom s = 0, so setze den BDD–Ausgang z = y und beende den Decodiervorgang für dieses Empfangswort.
- Andernfalls setze den Parameter r = 1 und mache mit Schritt (B) weiter.
(B) Bestimme die tatsächliche Symbolfehleranzahl r:
- Erstelle und überprüfe die Gleichungen Λl · sT = 0 für l = 1, ..., 2t–r unter der Annahme, dass das Empfangswort genau r Symbolfehler beinhaltet.
- Λl bezeichnet die verallgemeinerten ELP–Koeffizientenvektoren und t die Korrekturfähigkeit des Codes. Für die Reed–Solomon–Codes gilt einheitlich t = ⌊(n – k)/2⌋.
- Gibt es eine eindeutige Lösung, dann mache mit Schritt (C) weiter. Im Empfangsvektor y sind dann tatsächlich genau r Symbole verfälscht und im Fehlervektor e gibt es r Einträge ungleich 0.
- Andernfalls erhöhe r um 1. Falls r ≤ t, dann wiederhole Schritt (B) von Beginn an: Das bisher angenommene r war offensichtlich zu klein. Deshalb nun ein neuer Versuch mit größerem r.
- Ist das neue r größer als die Korrekturfähigkeit t des Codes, so kann das aktuelle Empfangswort nicht decodiert werden. Beende den Decodierversuch mit einer Fehlermeldung.
(C) Lokalisiere die r Fehlerpositionen:
- Erstelle das Error Locator Polynom Λ(x) und finde dessen r Nullstellen in GF(q) \ {0}.
- Ein Fehler an der Stelle i liegt immer dann vor, wenn Λ(αi) = 0 ist.
(D) Bestimme die r Fehlerwerte ei ≠ 0:
- Bekannt sind die r Fehlerstellen. Ersetzt man im Empfangsvektor y die falschen Symbole durch Auslöschungen ⇒ yi = E, falls ei ≠ 0, so findet man das Ergebnis z entsprechend Kapitel 2.4.
- Eine Alternative: Aus der Gleichung e · HT = s kommt man unter Ausnutzung der fehlerfreien Stellen (ei = 0) zu einem linearen Gleichungssystem für die fehlerhaften Symbole (ei ≠ 0).
Schritt (A): Auswertung des Syndroms beim BDD
Wie in Kapitel 1.5 gezeigt, kann zur Decodierung eines linearen Codes das Syndrom s herangezogen werden. Mit dem Empfangswort y gleich Codewort c plus Fehlervektor e gilt für dieses:
\[\underline {s} = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}= \underline {c} \cdot { \boldsymbol{\rm H }}^{\rm T}+ \underline {e} \cdot { \boldsymbol{\rm H }}^{\rm T} \hspace{0.05cm}.\]
Da stets c · HT = 0 gilt, folgt aus s = 0 auch e · HT = 0. Das heißt:
- Mit sehr großer Wahrscheinlichkeit kann aus s = 0 auch auf e = 0 und damit auch auf das richtige Decodierergebnis z = y geschlossen werden. Der Decodiervorgang wäre damit abgeschlossen.
- Es gibt aber auch Fehlermuster e ≠ 0, die zum Syndrom s = 0 führen. Solche Muster beinhalten sicher mehr als t Symbolfehler, so dass auch hier der Abbruch des Decodiervorgangs sinnvoll ist. Alle nachfolgenden Berechnungen würden auch nicht zum Erfolg führen.
 Diesem und den folgenden Beispielen auf den nächsten Seiten liegt stets der Reed–Solomon–Code (7, 3, 5)8 zugrunde, so dass die hier angegebenen Umrechnungen in GF(23) genutzt werden können. Das Empfangswort lautet:
Diesem und den folgenden Beispielen auf den nächsten Seiten liegt stets der Reed–Solomon–Code (7, 3, 5)8 zugrunde, so dass die hier angegebenen Umrechnungen in GF(23) genutzt werden können. Das Empfangswort lautet:
\[\underline{y}=\big (\alpha^3,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm}\alpha^1, \hspace{0.05cm} \alpha^2, \hspace{0.05cm} \alpha^5, \hspace{0.05cm} \alpha^5 \big).\]
Mit der Prüfmatrix H ergibt sich für das Syndrom:
\[\underline {s} \hspace{-0.15cm} = \hspace{-0.15cm} \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}= \begin{pmatrix} \alpha^3, \hspace{0.05cm}1, \hspace{0.05cm}0, \hspace{0.05cm}\alpha^1, \hspace{0.05cm}\alpha^2, \hspace{0.05cm}\alpha^5, \hspace{0.05cm}\alpha^5 \end{pmatrix}\cdot \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 \\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 \\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^5 \\ \alpha^4 & \alpha^1 & \alpha^5 & \alpha^2 \\ \alpha^5 & \alpha^3 & \alpha^1 & \alpha^6 \\ \alpha^6 & \alpha^5 & \alpha^4 & \alpha^3 \end{pmatrix} = \] \[ \hspace{-0.15cm} = \hspace{-0.15cm}(\alpha^3 , \alpha^3 , \alpha^3 , \alpha^3) + (\alpha^1 , \alpha^2 , \alpha^3 , \alpha^4) + (0,0,0,0) + (\alpha^4,1,\alpha^3,\alpha^6)+\] \[\hspace{0.15cm} + \hspace{0.15cm} (\alpha^6,\alpha^3,1,\alpha^4)+(\alpha^3,\alpha^1,\alpha^6,\alpha^4) + (\alpha^4,\alpha^3,\alpha^2,\alpha^1)= ... \hspace{0.05cm}= (\alpha^5,\alpha^2,\alpha^3,\alpha^1) \hspace{0.05cm}.\]
Das Empfangswort wurde also verfälscht. Andernfalls hätte sich s = 0 = (0, 0, 0, 0) ergeben müssen.
Error Locator Polynom – Definition und Eigenschaften (1)
Nach der Syndromberechnung mit dem Ergebnis s ≠ 0 wissen wir,
- dass das Empfangswort y nicht mit dem Codewort c übereinstimmt, bzw.
- dass der Fehlervektor e = (e0, e1, ... , en–1) auch Elemente ungleich 0 beinhaltet.
Wir wissen allerdings nicht, wie viele Symbole verfälscht wurden (0 < r ≤ n) und wir können auch nicht die Positionen der Fehlerstellen (ei ≠ 0) im Fehlervektor e nennen.
Einen Lösungsansatz für diese Aufgabe bietet das Error Locator Polynom, das von W. W. Peterson eingeführt wurde. Siehe [Pet60][1]. Im Deutschen ist hierfür auch der Begriff Schlüsselgleichung üblich.
\[I_{\rm FP} = \{ i \hspace{0.1cm}| \hspace{0.1cm} e_i \ne 0,\hspace{0.1cm} 0 \le i < n \}\hspace{0.05cm}.\]
Dann gilt für das Error Locator Polynom (ELP):
\[{\it \Lambda}(x)=x \cdot \prod_{i\hspace{0.05cm}\in \hspace{0.05cm} I_{\rm FP}}(x-\alpha^i) =x \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+\ldots+{\it \lambda}_{r-1} \cdot x^{r-1}+x^r \big ].\]
Vom Error Locator Polynom wissen wir aufgrund der Definition:
- Wegen des Faktors x vor dem Produktzeichen ist Λ(x = 0) = 0.
- Weitere r Nullstellen ergeben sich für x = αi mit i ∈ IFP, das heißt, für alle Fehlerpositionen.
- Dagegen ergibt das Error Locator Polynom für i ∉ IFP ⇒ ei = 0 keine Nullstelle: Λ(x = αi) ≠ 0.
Wir suchen also die r nichttrivialen Nullstellen von Λ(x) mit dem Argument x ∈ GF(q) \ {0}. Gelingt uns dies, so kennen wir die r Fehlerpositionen, jedoch noch nicht die tatsächlichen Fehlerwerte ei ∈ GF(q).
 Es gelte n = 7 ⇒ q = 8, r = 2 und IFP = {2, 4}:
Es gelte n = 7 ⇒ q = 8, r = 2 und IFP = {2, 4}:
Damit erhält man für das Error Locator Poynom aus GF(23):
\[{\it \Lambda}(x)\hspace{0.15cm} = \hspace{0.15cm}x \cdot (x-\alpha^2) \cdot (x-\alpha^4)=\] \[ \hspace{1.1cm} = \hspace{0.15cm} x \cdot (x+\alpha^2) \cdot (x+\alpha^4) =\] \[ \hspace{1.1cm} = \hspace{0.15cm}x \cdot \big [x^2 + (\alpha^2 + \alpha^4) \cdot x + \alpha^6\big ] =\] \[ \hspace{1.1cm} = \hspace{0.15cm} x \cdot \big [\alpha^6 + \alpha \cdot x + x^2\big ]\hspace{0.05cm}.\]
Die beiden Nullstellen (außer bei x = 0) ergeben sich hier natürlich für x = α2 und x = α4, wie die folgende Kontrollrechnung zeigt:
\[{\it \Lambda}(x = \alpha^2)\hspace{-0.15cm} = \hspace{-0.15cm} x \cdot \big [\alpha^6 + \alpha \cdot \alpha^2 + (\alpha^2)^2\big ] = x \cdot \big [\alpha^6 + \alpha^3 + \alpha^4 \big ]= 0\hspace{0.05cm},\]
\[ {\it \Lambda}(x = \alpha^4)\hspace{-0.15cm} = \hspace{-0.15cm} x \cdot \big [\alpha^6 + \alpha \cdot \alpha^4 + (\alpha^4)^2\big ] =x \cdot \big [\alpha^6 + \alpha^5 + \alpha \big ]= 0\hspace{0.05cm}.\]
Error Locator Polynom – Definition und Eigenschaften (2)
Für die weitere Herleitung gehen wir stets vom RSC (7, 3, 5)8 mit den folgenden Parameterwerten aus: n = 7, k = 3, dmin = 5 ⇒ t = (dmin – 1)/2 = 2. Die Anzahl der Symbolfehler sei r = 2 = t.
Damit lautet das zu lösende Gleichungssystem mit den Hilfsgrößen Ai = Λ(αi):
\[A_0 = {\it \Lambda }(\alpha^0) \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^0 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^0)^1 + (\alpha^0)^2 \right ] = {\it \lambda}_0 \cdot 1 + {\it \lambda}_1 \cdot 1 + 1 \hspace{0.05cm},\] \[A_1 = {\it \Lambda }(\alpha^1) \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^1 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^1)^1 + (\alpha^1)^2 \right ] = {\it \lambda}_0 \cdot \alpha^1+ {\it \lambda}_1 \cdot \alpha^2 + \alpha^3 \hspace{0.05cm},\]
- \[...\]
\[ A_6 = {\it \Lambda }(\alpha^6) \hspace{-0.15cm} = \hspace{-0.15cm} \alpha^6 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^6)^1 + (\alpha^6)^2 \right ] = {\it \lambda}_0 \cdot \alpha^6 + {\it \lambda}_1 \cdot \alpha^{12} + \alpha^{18} \hspace{0.05cm}.\]
In Vektorform lautet dieses Gleichungssystem mit dem Hilfsvektor A = (A0, A1, A2, A3, A4, A5, A6):
\[\underline {A}^{\rm T}=\begin{pmatrix} A_0\\ A_1\\ A_2\\ A_3\\ A_4\\ A_5\\ A_6 \end{pmatrix} \hspace{0.15cm} = \hspace{0.15cm} \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^9 \\ \alpha^4 & \alpha^8 & \alpha^{12}\\ \alpha^5 & \alpha^{10} & \alpha^{15}\\ \alpha^6 & \alpha^{12} & \alpha^{18} \end{pmatrix} \hspace{0.15cm}\cdot \hspace{0.15cm} \begin{pmatrix} {\lambda}_0\\ {\lambda}_1\\ 1 \end{pmatrix} \hspace{0.05cm}.\]
Wir erweitern nun den ELP–Koeffizientenvektor Λ durch Anhängen von Nullen auf die Länge n – k. Im betrachteten Beispiel erhält man somit Λ = (λ0, λ1, 1, 0) und folgende Vektorgleichung:
\[\underline {A}^{\rm T} \hspace{0.15cm} = \hspace{0.15cm} \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^8\\ \alpha^3 & \alpha^6 & \alpha^9 & \alpha^{12}\\ \alpha^4 & \alpha^8 & \alpha^{12} & \alpha^{16}\\ \alpha^5 & \alpha^{10} & \alpha^{15} & \alpha^{20}\\ \alpha^6 & \alpha^{12} & \alpha^{18} & \alpha^{24} \end{pmatrix} \hspace{0.15cm}\cdot \hspace{0.15cm} \begin{pmatrix} {\lambda}_0\\ {\lambda}_1\\ 1\\ 0 \end{pmatrix} \hspace{0.05cm}.\]
Aus der 7 × 3–Matrix wurde nun eine 7 × 4–Matrix. Ddie vierte Spalte kann eigentlich beliebig gefüllt werden, da alle Elemente mit Nullen multipliziert werden. Durch die hier gewählte Ergänzung erhält man die transponierte Prüfmatrix des RSC (7, 3, 5)8, und man kann für die letzte Vektorgleichung schreiben:
\[\underline {A}^{\rm T} = { \boldsymbol{\rm H }}^{\rm T} \cdot \underline {\it \Lambda }^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline {A} = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} \hspace{0.05cm}.\]
Da aber für die Fehlerstellen (ei ≠ 0) stets Ai = Λ(αi) = 0 gilt, ist das Produkt Ai · ei immer 0 und man erhält als Bestimmungsgleichung für die Nullstellen des Error Locator Polynoms:
\[\underline {A}^{\rm T} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {\it \Lambda } \cdot \underline {s}^{\rm T} = 0 \hspace{0.05cm}.\]
Daraus folgt das wichtige Zwischenergebnis: Die nichttrivialen Nullstellen (ungleich 0) λ0, λ1, ... des Error Locator Polynoms Λ(x) müssen stets der Vektorgleichung Λ · sT = 0 genügen, wobei Λ den ELP–Koeffizientenvektor bezeichnet und s = y · HT das Syndrom angibt.
Schritt (B): Aufstellen/Auswerten des ELP–Koeffizientenvektors (1)
Bevor wir das Zwischenergebnis Λ · sT = 0 an einem Beispiel verdeutlichen können, müssen noch einige Verallgemeinerungen vorgenommen werden. Der Grund hierfür ist:
- Die Gleichung Λ · sT = 0 liefert nur eine einzige Bestimmungsgleichung. Damit kann das Problem für r = 1 gelöst werden, wenn man sicher ist, dass tatsächlich nur ein Symbol verfälscht wurde.
- Ist man sich dessen nicht sicher, führt aber die Berechnung trotzdem für r = 1 durch, so braucht man noch eine zweite Gleichung (oder auch mehrere), um die Annahme zu verifizieren.
Die Eigenschaft des Error Locator Polynoms, dass Λ(αi) nur für ei ≠ 0 (i–tes Symbol verfälscht) gleich Null ist, bleibt erhalten, wenn man Λ(x) mit beliebigen Potenzen von x multipliziert. Jede Multiplikation mit x bedeutet für den ELP–Koeffizientenvektor eine Verschiebung um eine Stelle nach rechts.
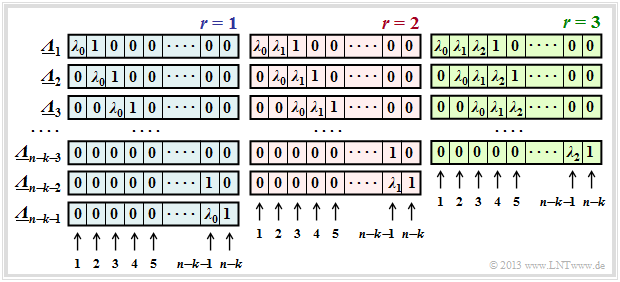
Mit der verallgemeinerten Definition (wobei Λ1(x) dem bisherigen Λ(x) entspricht),
\[{\it \Lambda}_l(x)=x^l \cdot \prod_{i\hspace{0.05cm}\in \hspace{0.05cm} I_{\rm FP}}(x-\alpha^i) =x^l \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+\ldots+{\it \lambda}_{r-1} \cdot x^{r-1}+x^r \big ]\hspace{0.05cm},\]
ergeben sich durch sukzessive Verschiebung gegenüber Λ die ELP–Koeffizientenvektoren Λl. Die Grafik zeigt die Belegung unter der Annahme von 1 ≤ r ≤ 3 Fehlerstellen im Vektor e. Man erkennt:
- Die Länge aller Λl ist stets n – k. Jeder Vektor beinhaltet jeweils r Koeffizienten λi(0 ≤ i < r) und eine Eins. Der Rest eines jeden Vektors ist mit Nullen aufgefüllt.
- Für jedes r gibt es genau n–k–r Koeffizientenvektoren Λl, wobei sich Λl aus Λl–1 stets durch Rechtsverschiebung um eine Position ergibt. Der Vektor Λn–k–r endet immer mit einer 1.
- Das Gleichungssystem Λl · sT = 0 führt deshalb zu n – k – r Gleichungen. Der gewählte Ansatz für r ist nur dann richtig, wenn alle Gleichungen zu den gleichen Ergebnissen für λ0, ... , λr–1 führen.
- Ist dies nicht der Fall, so muss man r erhöhen und damit ein neues Gleichungssystem bearbeiten, und zwar solange, bis sich aus allen Gleichungen für das aktuelle r eine eindeutige Lösung ergibt.
- Ist schließlich r größer als die Korrekturfähigkeit t des Codes, so kann die Berechnung beendet werden. Das anstehende Empfangswort y ist dann nicht decodierbar.
Schritt (B): Aufstellen/Auswerten des ELP–Koeffizientenvektors (2)
Hier nochmals die verallgemeinerte Definition für das Error Locator Polynom (ELP):
\[{\it \Lambda}_l(x)=x^l \cdot \prod_{i\hspace{0.05cm}\in \hspace{0.05cm} I_{\rm FP}}(x-\alpha^i) =x^l \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+\ldots+{\it \lambda}_{r-1} \cdot x^{r-1}+x^r \big ]\hspace{0.05cm}.\]
Dieses lässt sich am einfachsten mit den verschobenen ELP–Koeffizientenvektoren Λl auswerten, wie im folgenden Beispiel gezeigt wird. Hierbei beziehen wir uns auf die Grafik auf der letzen Seite, die Λl–Belegung unter der Annahme r = 1, r = 2 oder r = 3 Fehler im Fehlervektor e zeigt.
Unter der Annahme eines einzigen falschen Symbols (r = 1) erhält man folgendes Gleichungssystem (hier in Matrixform geschrieben):
\[\big ({ \boldsymbol{\it \Lambda }}_l \big) \cdot \underline {s} ^{\rm T}= \begin{pmatrix} \lambda_0 & 1 & 0 & 0 \\ 0 & \lambda_0 & 1 & 0 \\ 0 & 0 & \lambda_0 & 1 \end{pmatrix} \cdot \begin{pmatrix} \alpha^5\\ \alpha^2\\ \alpha^3\\ \alpha \end{pmatrix} \stackrel{!}{=} \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \hspace{0.05cm}\]
\[\Rightarrow \hspace{0.3cm}\alpha^5 \cdot \lambda_0 + \alpha^2 \hspace{-0.15cm} = \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{2-5}= \alpha^{-3}= \alpha^{4}\hspace{0.05cm},\] \[\hspace{0.8cm}\alpha^2 \cdot \lambda_0 + \alpha^3 \hspace{-0.15cm} = \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{3-2}= \alpha\hspace{0.05cm},\] \[\hspace{0.8cm}\alpha^3 \cdot \lambda_0 + \alpha^1 \hspace{-0.15cm} = \hspace{-0.15cm} 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{1-3}= \alpha^{-2} = \alpha^{5} \hspace{0.05cm}.\]
Diese drei Gleichungen liefern drei unterschiedliche Lösungen für λ0, was nicht zielführend ist.
Deshalb stellen wir nun ein weiteres Gleichungssystem auf, und zwar unter der Annahme r = 2:
\[\big ({ \boldsymbol{\it \Lambda }}_l \big) \cdot \underline {s} ^{\rm T}= \begin{pmatrix} \lambda_0 & \lambda_1 & 1 & 0 \\ 0 & \lambda_0 & \lambda_1 & 1 \end{pmatrix} \cdot \begin{pmatrix} \alpha^5\\ \alpha^2\\ \alpha^3\\ \alpha \end{pmatrix} \stackrel{!}{=} \begin{pmatrix} 0\\ 0 \end{pmatrix} \]
\[\Rightarrow \hspace{0.3cm}\alpha^5 \cdot \lambda_0 + \alpha^2 \cdot \lambda_1 + \alpha^3 \hspace{-0.15cm} = \hspace{-0.15cm} 0 \hspace{0.05cm},\] \[\hspace{0.8cm}\alpha^2 \cdot \lambda_0 + \alpha^3 \cdot \lambda_1 + \alpha^1 \hspace{-0.15cm} = \hspace{-0.15cm} 0 \hspace{0.05cm}.\]
Dieses Gleichungssystem ist nun eindeutig lösbar. Man erhält λ0 = α2 und λ1 = α6. Das bedeutet: Die Annahme, dass tatsächlich r = 2 Positionen des Empfangsvektors y verfälscht wurden, ist richtig.
Schritt (C): Lokalisierung der Fehlerstellen
Nach Abarbeitung von Schritt (B) sind bekannt:
- die Anzahl r der Fehlerstellen ei ≠ 0 im Vektor e = (e0, ... , ei, ... , en–1),
- die Koeffizienten λ0, ... , λr–1 des Error Locator Polynoms.
Zu bestimmen ist nun noch die Menge der Fehlerpositionen:
\[I_{\rm FP} = \{ i \hspace{0.1cm}| \hspace{0.1cm} e_i \ne 0,\hspace{0.1cm} 0 \le i < n \}\hspace{0.05cm}.\]
Hierzu gibt es zwei Möglichkeiten:
- die so genannte Chien–Suche, in dem man durch Einsetzen der möglichen Codesymbole außer dem Nullsymbol ⇒ αi (0 ≤ i < n) in das Error Locator Polynom dessen Nullstellen er- mittelt,
- die Auswertung der Gleichung A = (A0, ... , Ai, ... , An–1) = Λ · H mit der Abkürzung Ai = Λ(αi).
Beide Verfahren werden im folgenden Beispiel angewendet.
\[{\it \Lambda}(x)=x \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+x^2 \big ] =x \cdot \big [\alpha^2 + \alpha^6 \cdot x+x^2 \big ]\hspace{0.05cm}.\]
 Entsprechend der Chien–Suche erhält man
Entsprechend der Chien–Suche erhält man
\[{\it \Lambda}(\alpha^0)\hspace{0.15cm} = \hspace{0.15cm}\alpha^0 \cdot \big [ \alpha^2 + \alpha^6 \cdot 1 + 1 \big ] = \] \[\hspace{1.4cm} = \hspace{0.15cm} \alpha^2 + (\alpha^2 + 1) + 1 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Nullstelle}}\hspace{0.05cm},\] \[{\it \Lambda}(\alpha^1)\hspace{0.15cm} = \hspace{0.15cm}\alpha^1 \cdot \big [\alpha^2 + \alpha^6 \cdot \alpha^1 + \alpha^2\big ]=\] \[\hspace{1.4cm} = \hspace{0.15cm} \alpha^1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm Keine\hspace{0.15cm} Nullstelle}\hspace{0.05cm},\] \[{\it \Lambda}(\alpha^2)\hspace{0.15cm} = \hspace{0.15cm}\alpha^2 \cdot \big [ \alpha^2 + \alpha^6 \cdot \alpha^2 + \alpha^4 \big ] =\alpha^4 + \alpha^{10} + \alpha^6 =\] \[ \hspace{1.4cm} = \hspace{0.15cm} (\alpha^2 + \alpha) + (\alpha + 1) + (\alpha^2 + 1) =\] \[ \hspace{1.4cm}= \hspace{0.15cm}0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Nullstelle}}\hspace{0.05cm}.\]
Damit sind die beiden Fehlerpositionen mit i = 0 und i = 2 gefunden und der Fehlervektor lautet: e = (e0, 0, e2, 0, 0, 0, 0).
Die Vektorgleichung A = Λ · H liefert das gleiche Ergebnis in kompakterer Form:
\[\underline {A} \hspace{0.15cm} = \hspace{0.15cm} \underline{\it \Lambda} \cdot { \boldsymbol{\rm H }} = (\alpha^2, \alpha^6, 1, 0) \cdot \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6 \\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^3 & \alpha^5 \\ 1 & \alpha^3 & \alpha^6 & \alpha^3 & \alpha^5 & \alpha^1 & \alpha^4 \\ 1 & \alpha^4 & \alpha^1 & \alpha^5 & \alpha^2 & \alpha^6 & \alpha^3 \end{pmatrix} = \] \[ \hspace{0.5cm} = \hspace{0.15cm}(\alpha^2,\alpha^3,\alpha^4,\alpha^5,\alpha^6,1 ,\alpha^1) + (\alpha^6,\alpha^1,\alpha^3,\alpha^5,1 ,\alpha^2,\alpha^4)+\] \[ \hspace{0.5cm}+ \hspace{0.15cm} (1, \alpha^3,\alpha^6,\alpha^3,\alpha^5,\alpha^1,\alpha^4) = (0,\alpha^1,0,\alpha^3,\alpha^3,\alpha^5,\alpha^1)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} A_0 = A_2 = 0\hspace{0.05cm}.\]
Fortsetzung im Beispiel D auf der nächsten Seite.
Schritt (D): Abschließende Fehlerkorrektur
Im letzten Schritt müssen nun nur noch die r Symbolfehler korrigiert werden, deren Positionen nach Beendigung von Schritt (D) bekannt sind:
- Markiert man die Fehlerpositionen im Empfangswort y als Auslöschungen E (Erasures), so kann das zugehörige Codewort z entsprechend der Beschreibung im Kapitel 2.4 gefunden werden.
- Eine zweite Möglichkeit bietet die Bestimmung des Fehlervektors e aus der Gleichung e · HT = s und die Korrektur entsprechend z = y – e. Diese liegt dem folgenden Beispiel zugrunde.
Aus e · HT = s erhält man nun folgende Bestimmungsgleichungen für die Fehlerwerte e0 und e2:
\[\underline {e} \cdot { \boldsymbol{\rm H }}^{\rm T}= \begin{pmatrix} e_0 & 0 & e_2 & 0 & 0 & 0 & 0 \end{pmatrix}\cdot \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1\\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5}\\ \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2}\\ \alpha^5 & \alpha^{3} & \alpha^{1} & \alpha^{6}\\ \alpha^6 & \alpha^{5} & \alpha^{4} & \alpha^{3} \end{pmatrix} \stackrel{!}{=} \underline {s} = \begin{pmatrix} \alpha^5 & \alpha^2 & \alpha^3 & \alpha^1 \end{pmatrix} \]
\[\Rightarrow \hspace{0.3cm}e_0 \cdot (1, 1, 1, 1) + e_2 \cdot ( \alpha^2, \alpha^4, \alpha^6, \alpha^1)\stackrel{!}{=} ( \alpha^5, \alpha^2, \alpha^3, \alpha^1)\]
\[\Rightarrow \hspace{0.3cm} e_0 + e_2 \cdot \alpha^2 = \alpha^5\hspace{0.05cm},\hspace{0.2cm} e_0 + e_2 \cdot \alpha^4 = \alpha^2\hspace{0.05cm},\hspace{0.2cm} e_0 + e_2 \cdot \alpha^6 = \alpha^3\hspace{0.05cm},\hspace{0.2cm} e_0 + e_2 \cdot \alpha^1 = \alpha^1\hspace{0.05cm}.\]
 Alle diese Gleichungen führen zum Ergebnis e0 = 1, e2 = α2. Damit lautet das korrigierte Codewort:
Alle diese Gleichungen führen zum Ergebnis e0 = 1, e2 = α2. Damit lautet das korrigierte Codewort:
\[\hspace{0.8cm}\underline {y} \hspace{0.15cm} = \hspace{0.15cm} (\alpha^3,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} \alpha^1,\hspace{0.05cm} \alpha^2,\hspace{0.05cm} \alpha^5,\hspace{0.05cm} \alpha^5)\hspace{0.05cm},\] \[\hspace{0.8cm}\underline {e} \hspace{0.15cm} = \hspace{0.15cm} (1,\hspace{0.05cm} 0,\hspace{0.05cm} \alpha^2,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0)\hspace{0.05cm},\]
\[\Rightarrow \hspace{0.3cm}\underline {z} \hspace{0.15cm} = \hspace{0.15cm} \underline {y} - \underline {e} = \underline {y} + \underline {e}= (\alpha^1,\hspace{0.03cm} 1,\hspace{0.03cm} \alpha^2,\hspace{0.03cm} \alpha^1,\hspace{0.03cm} \alpha^2,\hspace{0.03cm} \alpha^5,\hspace{0.03cm} \alpha^5)\hspace{0.05cm}. \]
Schnelle Reed–Solomon–Decodierung
Die Klasse der Reed–Solomon–Codes wurde bereits im Jahre 1960 durch die Veröffentlichung [RS60][2] eingeführt. Ihre effiziente Decodierung war jedoch erst ein bis zwei Jahrzehnte später möglich.
Auf den letzten Seiten haben wir den so genannten Petersen–Algorithmus inklusive der Chien–Suche am Beispiel des RSC (7, 3, 5)8 demonstriert, der bis zu t = 2 Fehler korrigieren kann. Im Mittelpunkt des Decodiervorgangs stand dabei das Aufstellen und Lösen der Schlüsselgleichung (englisch: Error Locator Polynom), wobei die Nullstellen eines Grad–2–Polynoms in GF(7) gefunden werden mussten. Sie konnten erkennen, dass diese algebraische Decodierung mit großem Aufwand verbunden ist.
Bei den in Praxis eingesetzten Codes mit großer Codewortlänge n und hoher Korrekturfähigkeit t würde der Decodieraufwand explodieren, wenn nicht schnellere Decodieralgorithmen gefunden worden wären. So müssen beim Reed–Solomon–Code (255, 223, 33)256, der schon früh im ESA/NASA–Standard zur Satellitenübertragung genannt wurde, zur Decodierng eines einzigen Codewortes die bis zu t = 16 Nullstellen im GF(255) gefunden werden, und das auch noch in Echtzeit.
Ab Ende der 1960er Jahre haben sich viele Wissenschaftler um schnellere Decodieralgorithmen für Reed–Solomon–Codes bemüht:
- Beim Berlekamp–Massey–Algorithmus (BMA) wird die Schlüsselgleichung Λ · sT = 0 als rückgekoppeltes Schieberegister dargestellt, siehe zum Beispiel [Mas69][3], [Fri96][4] und [Bos98][5]. Das Problem wird damit auf die Synthese eines autoregressiven Filters zurückgeführt. Dieser Algorithmus arbeitet wesentlich schneller als der (leichter durchschaubare) Petersen–Algorithmus.
- Etwas später wurde in [SK+75][6] ein Decodierverfahren vorgeschlagen, das auf dem Euklidischen Algorithmus basiert. Dieser liefert den größten gemeinsamen Teiler zweier ganzer Zahlen, was zur Decodierung genutzt wird. Der Euklidische Algorithmus ist vergleichbar schnell wie der BMA. Genauere Informationen finden Sie wieder in [Bos98][7] und [Fri96][8].
- Weitere effiziente Decodiernethoden von Reed–Solomon–Codes arbeiten im Frequenzbereich unter Verwendung der Diskreten Fouriertransformation (DFT) im Körper GF(n).
Die Grundzüge der Reed–Solomon–Fehlerkorrektur wurden bereits in den 1960er Jahren entwickelt. Aber bis in die heutige Zeit (2013) ist die (möglichst schnelle) algebraische Decodierung dieser Codes ein hochaktuelles Forschungsgebiet.
Aufgaben
A2.12 Decodierung beim RSC(7, 4, 4)(Base 8)
Zusatzaufgaben:2.12 Reed–Solomon–Syndromberechnung
A2.13 Nun RSC (7, 3, 5)(Base 8)–Decodierung
Quellenverzeichnis
- ↑ Peterson, W.W: Encoding and Error-correction Procedures for the Bose-Chaudhuri codes. IRE Transactions on Information Theory , IT-6:459{470), 1960.
- ↑ Reed, I.S.; Solomon, G.: Polynomial Codes over Certain Finite Fields. J. Siam, Vol. 8, pp. 300–304, 1960.
- ↑ Massey, J.L.: Shift Register Synthesis and BCH Decoding.. IEEE Trans. on Information Theory, vol. IT-15, pp. 122–127, Jan. 1969.
- ↑ Friedrichs, B.: Kanalcodierung – Grundlagen und Anwendungen in modernen Kommunikations- systemen. Berlin – Heidelberg: Springer, 1996.
- ↑ Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998.
- ↑ Sugiyama, Y.; Kashara, M.; Hirasawa, S.; Namekawa, T.: A Method for Solving Key Equation for Decoding Goppa Codes. Information and Control, Vol. 27, pp. 87–99, 1975.
- ↑ Bossert, M.: Kanalcodierung. Stuttgart: B. G. Teubner, 1998.
- ↑ Friedrichs, B.: Kanalcodierung – Grundlagen und Anwendungen in modernen Kommunikations- systemen. Berlin – Heidelberg: Springer, 1996.