Exercise 4.7: Copper Twin Wire 0.5 mm

Hier soll das Zeitverhalten einer Kupferdoppelader mit Durchmesser $d = 0.5 \ \rm mm$ analysiert werden. Der Frequenzgang lautet mit der Leitungslänge $l = 1.5 \ \rm km$ und der Bitrate $R = 10 \rm Mbit/s$:

$$H_{\rm K}(f) = {\rm e}^{-{\rm a}_0 } \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} 2 \pi \cdot f \hspace{0.05cm} \cdot \hspace{0.01cm}\tau_{\rm P}} \cdot {\rm e}^{-{\rm a}_1 \hspace{0.05cm}\cdot \hspace{0.02cm}2f/R}\cdot {\rm e}^{-{\rm a}_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b_2 \hspace{0.05cm}\cdot \hspace{0.05cm}\sqrt{2f/R}} \hspace{0.05cm}.$$

Verwendet sind folgende Größen, die sich aus dem Dämpfungs– und Phasenmaß ableiten lassen: $${\rm a}_0 = \alpha_0 \cdot l\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm}\alpha_0 = 0.5066\,\, \frac{\rm Np}{\rm km}\hspace{0.05cm},$$ $$ \tau_{\rm P} = \frac{\beta_1 \cdot l}{2 \pi} \hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm}\beta_1 = 30.6\,\, \frac{\rm rad}{\rm km \cdot MHz}\hspace{0.05cm},$$ $$ {\rm a}_1 = \alpha_1 \cdot l \cdot {{R}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm} \alpha_1 = 0.136\,\, \frac{\rm Np}{\rm km \cdot MHz}\hspace{0.05cm},$$ $$ {\rm a}_2 = \alpha_2 \cdot l \cdot \sqrt{{R}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm} \alpha_2 = 1.1467\,\, \frac{\rm Np}{\rm km \cdot MHz^{0.5}}\hspace{0.05cm},$$ $$ {\rm b}_2 = \beta_2 \cdot l \cdot \sqrt{{R}/{2}}\hspace{0.05cm},\hspace{0.2cm}{\rm mit} \hspace{0.15cm} \beta_2 = 1.1467\,\, \frac{\rm rad}{\rm km \cdot MHz^{0.5}}\hspace{0.05cm}.$$

Die Impulsantwort lässt sich somit in der Form $$h_{\rm K}(t ) = K \cdot \left [ \delta(t - \tau_{\rm P})\star h_{1}(t) \star h_{2}(t) \right ]$$ darstellen, wobei

die Teilimpulsantwort $h_1(t)$ auf den dritten Term in obiger Gleichung zurückgeht, und
$h_2(t)$ die gemeinsame Zeitbereichsdarstellung der beiden letzten Terme angibt.

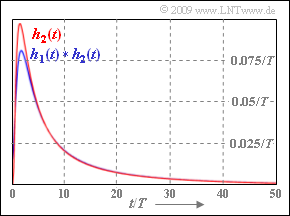
Die Grafik zeigt den Anteil $h_2(t)$ der Impulsantwort und das Faltungsprodukt $h_1(t) \star h_2(t)$. Dabei ist $h_2(t)$ gleich der Koaxialkabel–Impulsantwort mit der charakteristischen Kabeldämpfung ${\rm a}_\star = {\rm a}_2$.

Hinweise:

Die Aufgabe gehört zum Kapitel Eigenschaften von Kupfer–Doppeladern.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Die Parameter $\alpha_0$, $\alpha_1$ und $\alpha_2$ wurden aus den $k$–Parametern umgerechnet, wie in Aufgabe 4.6 gezeigt.
Der Phasenmaßparameter $\beta_2$ wurde hier zahlenmäßig gleich dem Dämpfungsmaßparameter $\alpha_2$ gesetzt. Der Dämpfungsanteil ${\rm a}_2$ und der Phasenanteil ${b}_2$ unterscheiden sich deshalb nur in der Einheit.
IAuf der Seite Diskussion der_gefundenen Näherungslösung wird dargelegt, warum diese Maßnahme erforderlich ist.

Fragebogen

$K \ =$

$\tau_P/T \ =$

$a_\star \ =$

$\ \rm dB$

	$h_{\rm 1}(t )$ ist eine gerade Funktion.
	Das Maximum von $h_{\rm 1}(t )$ liegt bei $t = 0$.
	Das Integral über $h_{\rm 1}(t )$ ergibt den Wert $2$.

	$h_1(t ) \star h_2(t )$ gibt die Verzerrungen von $h_{\rm K}(t )$ vollständig wieder.
	$h_1(t ) \star h_2(t )$ unterscheidet sich von $h_{\rm K}(t )$ nur durch einen Faktor.

Musterlösung

Solution

1. Mit a₀ = α₀ · l ≈ 0.76 Np erhält man für die Konstante K, die den Einfluss des Koeffizienten α₀ auf die Impulsantwort angibt:

$$K = {\rm e}^{-{\rm a}_0 }= {\rm e}^{-0.76} \hspace{0.15cm}\underline{= 0.468} \hspace{0.05cm}.$$

2. Für die Phasenlaufzeit gilt mit der angegebenen Gleichung:

$$\tau_{\rm P} = \frac{\beta_1 \cdot l}{2 \pi}= \frac{30.6 \cdot 1.5}{2 \pi}\, {\rm \mu s}\approx 7.31\, {\rm \mu s}\hspace{0.05cm},$$

und bezogen auf die Symboldauer T = 0.1 μs:

$${\tau_{\rm P}}/{T} \hspace{0.15cm}\underline{ \approx 73}\hspace{0.05cm}.$$

3. Die Impulsantwort eines Koaxialkabels ist näherungsweise gleich h₂(t), wenn dieses Koaxialkabel folgende charakteristische Kabeldämpfung aufweist:

$${\rm a}_\star ={\rm a}_2 = \alpha_2 \cdot l \cdot \sqrt{{R}/{2}} = 1.1467\,\, \frac{\rm Np}{\rm km \cdot MHz^{0.5}} \cdot 1.5\,{\rm km} \cdot \sqrt{\frac{10\,{\rm MHz}}{2}}=\\ = 2.93\,{\rm Np} = 2.93\,{\rm Np} \cdot8.686\,\frac {\rm dB}{\rm Np} \hspace{0.15cm}\underline{ =25.5\,{\rm dB}}\hspace{0.05cm}.$$

4. Richig sind die Aussagen 1 und 2. Die Fouriertransformierte H₁(f) = e^{–A · |f|} mit A = 2a₁/R ist reell und gerade, so dass h(t) ebenfalls reell und gerade ist. Aufgrund der Tiefpass–Charakteristik von H₁(f) liegt das Maximum bei t = 0. Dagegen ist die letzte Aussage falsch: Das Integral über h₁(t) im Bereich von ± ∞ ist gleich H₁(f = 0), also 1.

5. Richtig ist nur der Lösungsvorschlag 1: Die Teilimpulsantwort h₁(t) ∗ h₂(t) berücksichtigt den Einfluss von α₁, α₂ und β₂ und damit alle Terme, die zu Verzerrungen führen. Dagegen führt α₀ nur zu einer frequenzunabhängigen Dämpfung und β₁ zu einer für alle Frequenzen konstanten Laufzeit.

Der Lösungsvorschlag 2 trifft dagegen nicht zu. Zunächst (bei kleinen t–Werten) ist h₁(t) ∗ h₂(t) kleiner als h₂(t). Bei großen t–Werten liegt dann die blaue Kurve oberhalb der roten. Das bedeutet: a₁ und damit auch h₁(t) bewirken tatsächlich zusätzliche Verzerrungen, auch wenn diese nicht ins Gewicht fallen.