Exercise 4.4Z: Contour Lines of the "2D-PDF"

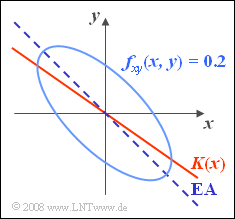
Gegeben ist eine zweidimensionale Gaußsche Zufallsgröße (x, y) mit dem Mittelwert (0, 0) und der 2D–WDF

$$f_{xy}(x,y) = C\cdot\rm e^{-(\it x^{\rm 2} + \it y^{\rm 2} +\sqrt{\rm 2}\cdot \it x\cdot\it y)}.$$

Bekannt ist weiterhin, dass die beiden Streuungen σ_x und σ_y jeweils gleich 1 sind. In der Skizze eingetragen sind:

eine Höhenlinie dieser WDF für f_xy(x, y) = 0.2,

die Ellipsenhauptachse (EA), und

die Korrelationsgerade y = K(x).

Hinweis: Die Aufgabe bezieht sich auf den Inhalt von Kapitel 4.2. Die hier behandelte Thematik ist zudem in zwei Lernvideos zusammengefasst:

Fragebogen

$\rho_\text{xy}$ =

$C$ =

$a$ =

$x_0/y_0$ =

	Die Korrelationsgerade ist steiler als die Ellipsenhauptachse.
	Der Winkel von K(x) gegenüber der x-Achse ist etwa –35°.
	Die Korrelationsgerade schneidet alle Höhenlinien dort, wo an die Ellipse eine vertikale Tangente angelegt werden kann.

Musterlösung

Solution

1. Auch ohne die Angabe „σ_x = σ_y = 1” könnte man erkennen, dass die beiden Streuungen gleich sind, da im Exponenten der 2D–WDF f_xy(x, y) die Koeffizienten bei x² und y² gleich sind. Durch Koeffizientenvergleich erhält man mit σ_x = σ_y = 1:

$$\frac{- 2 \rho_{xy}}{\sigma_x\cdot\sigma_y} = \sqrt{2}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \rho_{xy}=\frac{-1}{\sqrt{2}} \hspace{0.15cm}\underline{\approx -0.707}.$$

2. Mit den unter Punkt (1) berechneten Zahlenwerten erhalten wir:

$$C=\frac{\rm 1}{\rm 2\it\pi\cdot\sigma_x\cdot\sigma_y\cdot\sqrt{\rm 1 - \rho_{xy}^{\rm 2}}} =\frac{\rm 1}{\rm 2\pi\cdot\rm 1\cdot 1\cdot\sqrt{0.5}}=\frac{\rm 1}{\sqrt{\rm 2}\cdot \pi}\hspace{0.15cm}\underline{\approx \rm 0.225}.$$

3. Die allgemeine Gleichung lautet:

$$\alpha = \frac{\rm 1}{\rm 2}\cdot \rm arctan(\rm 2 \cdot\it \rho_{xy}\cdot \frac{\sigma_x\cdot\sigma_y}{\sigma_x^{\rm 2} - \sigma_y^{\rm 2}}).$$

Gilt σ_x = σ_y und ρ_xy ≠ 0, so ist der Winkel α stets ±45°. Das Vorzeichen ist abhängig vom Vorzeichen von ρ_xy. Im vorliegenden Fall gilt α = –45°.

4. Für die eingezeichnete Höhenlinie gilt:

$$f_{xy}(x, y)=\frac{\rm 1}{\sqrt{\rm 2}\cdot \pi}\cdot \rm e^{-(\it x^{\rm 2} + \it y^{\rm 2} + \sqrt{\rm 2}\cdot\it x\cdot\it y)}=\rm 0.2$$

$$\Rightarrow {\rm e}^{-(\it x^{\rm 2} + \it y^{\rm 2} + \sqrt{\rm 2}\cdot\it x\cdot\it y)} = \rm 0.8885 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} \it x^{\rm 2} + \it y^{\rm 2} + \sqrt{\rm 2}\cdot\it x\cdot\it y = -{\rm ln(0.8885)} \approx\rm 0.118.$$

Der Winkel der Ellipsenhauptachse ist –45°. Deshalb muss y₀ = –x₀ gelten. Daraus folgt weiter:

$$x_{\rm 0}^{\rm 2} + (-x_{\rm 0})^{\rm 2} + \sqrt{\rm 2}\cdot x_{\rm 0}(-x_{\rm 0}) = 0.118$$

$$\Rightarrow (\rm 2 - \sqrt{\rm 2})\cdot \it x_{\rm 0}^{\rm 2} = {\rm 0.118} \hspace{0.5cm}\Rightarrow \hspace{0.5cm} x_{\rm 0}^{\rm 2} \approx \frac{\rm0.118}{\rm0.585}\approx\rm 0.202; \hspace{0.5cm} x_{\rm 0}\approx\pm\rm 0.450.$$

Die beiden Schnittpunkte der eingezeichneten Höhenlinien mit der Ellipsenhauptachse liegen somit bei (0.45, –0.45) und (–0.45, 0.45). Der Quotient x₀/y₀ ist in beiden Fällen –1.

5. Vorweg das Ergebnis: Richtig sind die Lösungsvorschläge 2 und 3.

Mit σ_y = σ_x und dem Ergebnis aus (1) gilt für den Winkel der Korrelationsgeraden:

$$\theta_{y\rightarrow x} = \rm arctan (\it \rho_{\it xy})=\rm arctan(-\frac{\rm 1}{\sqrt{\rm 2}})\approx -\rm 35.3^{\circ}.$$

Das bedeutet: Die erste Aussage ist falsch und die zweite richtig. Nachfolgend der Beweis für die Richtigkeit der Aussage 3: Löst man die Ellipsengleichung (mit z = 0.118), also

$$x^{\rm 2}+ y^{\rm 2} +\sqrt{\rm 2}\cdot \it x\cdot \it y - \it z = \rm 0 ,$$

nach y auf, so erhält man nach Lösung einer quadratischen Gleichung

$$y_{\rm 1/2}=\frac{\sqrt{\rm 2}}{\rm 2}\it x\pm\sqrt{\frac{x^{\rm 2}}{\rm 2}-x^{\rm 2}+\it z} \hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_{\rm 1/2}=\frac{\it x}{\sqrt{\rm 2}}\pm \sqrt{\it z-\frac{x^{\rm 2}}{\rm 2}}.$$

Die vertikale Tangente ergibt sich für den Fall, dass die beiden Lösungen y_1/2 identisch sind. Das heißt: der Wurzelausdruck muss den Wert 0 ergeben. Die Lösung für positives x lautet dann:

$$x_{\rm T}=\sqrt{\rm 2\cdot \it z}=\rm \rm 0.485.$$

Eingesetzt in die Ellipsengleichung erhält man für den y-Wert des Tangentialpunktes:

$$x_{\rm T}^{\rm 2} + y_{\rm T}^{\rm 2} + \sqrt{\rm 2}\cdot\it x_{\rm T} \cdot y_{\rm T} - \it z = \rm 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm}\rm 2 \it z + y_{\rm T}^{\rm 2} + \rm 2\sqrt{\it z}\cdot\it y_{\rm T} - \it z = \rm 0$$

$$\Rightarrow y_{\rm T}^{\rm 2} + \rm 2\sqrt{\it z}\cdot\it y_{\rm T} + \it z = \rm 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} (y_{\rm T} + \sqrt{\it z}) = \rm 0\hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_{\rm T} = -\sqrt{\it z} = -0.343.$$

Daraus ergibt sich:

$$y_{\rm T}=-\frac{\it x_{\rm T}}{\sqrt{\rm 2}}.$$

Das bedeutet aber auch: Der Tangentialpunkt (x_T, y_T) liegt exakt auf der Korrelationsgeraden:

$$y=K(x)=-{\it x}/{\sqrt{\rm 2}}.$$