Exercise 5.1: Sampling Theorem

• Return to book

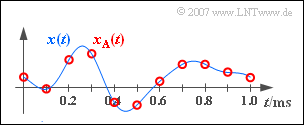
Gegeben ist ein Analogsignal $x(t)$ entsprechend der Skizze.

• Bekannt ist, dass dieses Signal keine höheren Frequenzen als $B_{\rm NF} = 4 \ \text{kHz}$ beinhaltet.
• Durch Abtastung mit der Abtastrate $f_{\rm A}$ erhält man das in der Grafik rot eingezeichnete Signal $x_{\rm A}(t)$.
• Zur Signalrekonstruktion wird ein Tiefpass verwendet, für dessen Frequenzgang gilt:

$$H(f) = \left\{ \begin{array}{c} 1 \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c} {\rm{{\rm{f\ddot{u}r}}}} \\ {\rm{{\rm{f\ddot{u}r}}}} \\ \end{array}\begin{array}{*{5}c} |f| < f_1 \hspace{0.05cm}, \\ |f| > f_2 \hspace{0.05cm} \\ \end{array}$$

Der Bereich zwischen den Frequenzen $f_1$ und $f_2 > f_1$ ist für die Lösung dieser Aufgabe nicht relevant.

Die Eckfrequenzen $f_1$ und $f_2$ sind so zu bestimmen, dass das Ausgangssignal $y(t)$ des Tiefpasses mit dem Signal $x(t)$ exakt übereinstimmt.

Hinweise:

• Die Aufgabe gehört zum Kapitel Zeitdiskrete Signaldarstellung.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Zu der hier behandelten Thematik gibt es auch ein Interaktionsmodul:

Abtastung periodischer Signale und Signalrekonstruktion

Fragebogen

1

Ermitteln Sie aus der Grafik die zugrundeliegende Abtastrate.

$f_{\rm A}$   =  $\text{kHz}$

2

Bei welchen Frequenzen besitzt die Spektralfunktion $X_{\rm A}(f)$ mit Sicherheit keine Anteile?

	$f = 2.5 \ \text{kHz},$
	$f= 5.5 \text{kHz},$
	$f= 6.5 \text{kHz},$
	$f= 34.5 \text{kHz}.$

3

Wie groß muss die untere Eckfrequenz $f_1$ mindestens sein, damit das Signal perfekt rekonstruiert wird?

$f_{1,\ \text{min}}$   =  $\text{kHz}$

4

Wie groß darf die obere Eckfrequenz $f_2$ höchstens sein, damit das Signal perfekt rekonstruiert wird?

$f_{2,\ \text{max}}$   =  $\text{kHz}$

Musterlösung

Solution

1. Der Abstand zweier benachbarter Abtastwerte beträgt $T_{\rm A} = 0.1 \ \text{ms}$. Somit erhält man für die Abtastrate $f_{\rm A} = 1/ T_{\rm A} \;\underline {= 10 \ \text{kHz}}$.

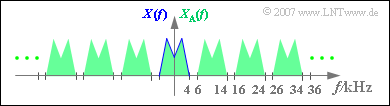
2. Das Spektrum $X_{\rm A}(f)$ des abgetasteten Signals erhält man aus $X(f)$ durch periodische Fortsetzung im Abstand $f_{\rm A} = 10 \ \text{kHz}$. Aus der Skizze erkennt man, dass $X_{\rm A}(f)$ durchaus Anteile bei $f = 2.5 \ \text{kHz}$ und $f = 6.5 \ \text{kHz}$besitzen kann, nicht jedoch bei $f = 5.5 \ \text{kHz}$. Auch bei $f = 34.5 \ \text{kHz}$ wird $X_{\rm A}(f)$ = 0 auf jeden Fall gelten. Richtig sind also die Lösungsvorschläge 2 und 4.

3. Es muss sichergestellt sein, dass alle Frequenzen des Analogsignals mit $H(f) = 1$ bewertet werden. Daraus folgt entsprechend der siehe Skizze:

$$f_{1, \ \text{min}} = B_{\rm NF} \;\underline{= 4 \ \text{kHz}}.$$

4. Ebenso muss garantiert werden, dass alle Spektralanteile von $X_{\rm A}(f)$, die in $X(f)$ nicht enthalten sind, durch den Tiefpass entfernt werden. Entsprechend der Skizze gilt:

$$f_{2, \ \text{max}} = f_{\rm A} – B_{\rm NF} \;\underline{= 6 \ \text{kHz}}.$$