Exercise 5.4Z: On the Hanning Window

• Return to book

In dieser Aufgabe sollen wichtige Eigenschaften des häufig verwendeten Hanning–Fensters hergeleitet werden. Die zeitkontinuierliche Darstellung im Intervall von $–T_{\rm P}/2$ bis $+T_{\rm P}/2$ lautet hier wie folgt: $$w(t)= {\rm cos}^2(\pi \cdot {t}/{T_{\rm P}})= 0.5\cdot \left(1 + {\rm cos}(2\pi \cdot {t}/{T_{\rm P}}) \right ) \hspace{0.05cm}.$$ Außerhalb des symmetrischen Zeitbereichs der Dauer $T_{\rm P}$ ist $w(t) \equiv 0$.

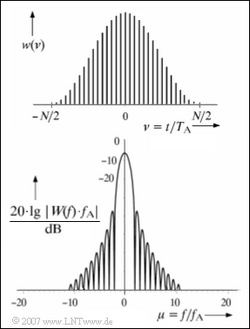
Die obere Grafik zeigt die zeitdiskrete Darstellung $w(\nu) = w({\nu} \cdot T_{\rm A})$, wobei $T_{\rm A}$ um den Faktor $N = 32$ kleiner ist als $T_{\rm P}$. Der Definitionsbereich der diskreten Zeitvariablen $ν$ reicht von $–16$ bis $+15$.

In der unteren Grafik ist die Fouriertransformierte $W(f)$ der zeitkontinuierlichen Fensterfunktion $w(t)$ logarithmisch dargestellt. Die Abszisse ist hierbei auf $f_{\rm A} = 1/T_{\rm P}$ normiert ist. Man erkennt:

• Die äquidistanten Werte $W({\mu} \cdot f_{\rm A})$ sind $0$ mit Ausnahme von $μ = 0$ und $μ = ±1$.
• Die Hauptkeule erstreckt sich somit auf den Frequenzbereich $|f| ≤ 2 · f_{\rm A}$.
• $W(f)$ ist außerhalb der Hauptkeule betragsmäßig für $f = ±2.5 · f_{\rm A}$ am größten.
• Somit gilt hier für den minimalen Abstand zwischen Haupt– und Seitenkeulen:

$$A_{\rm H/S} = 20 \cdot {\rm lg}\hspace{0.15cm} \frac{|W(0)|}{|W(2.5 \cdot f_{\rm A})|} \hspace{0.15cm}{\rm (in}\hspace{0.1cm}{\rm dB)}\hspace{0.05cm}.$$

Hinweise:

• Die Aufgabe gehört zum Kapitel Spektralanalyse.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Geben Sie die zeitdiskreten Koeffizienten $w(ν)$ des Hanning–Fensters analytisch an. Welche Zahlenwerte ergeben sich für $ν = 0$, $ν = 1$ und $ν = -\hspace{0.05cm}8$?

$w(ν = 0) \ =$

$w(ν = 1) \ =$

$w(ν = -\hspace{0.05cm}8) \ =$

2

Berechnen Sie die Spektralfunktion $W(f)$ allgemein. Welche der folgenden Aussagen sind zutreffend??

	$W(f)$ liefert für spezielle Frequenzwerte komplexe Ergebnisse.
	$W(f)$ ist bezüglich $f$ gerade, das heißt, es gilt stets $W(–f) = W(f)$.
	Der Spektralwert $W(f = 0)$ ist gleich $0.5/f_{\rm A}$ und somit reell.

3

Wie groß sind $W(f = ±f_{\rm A})$ und die auf $f_{\rm A}$ normierte 6 dB–Bandbreite?

$B_{\rm 6\hspace{0.05cm}dB}\hspace{-0.05cm}/\hspace{-0.05cm}f_{\rm A} \ =$

4

Wie groß ist der minimale Abstand zwischen Hauptkeule und Seitenkeule.

$A_{\rm H/S} \ =$ $\ \rm dB$

Musterlösung

Solution

(1)  Nach trigonometrischer Umformung ergibt sich für die zeitkontinuierliche Fensterfunktion: $$w(t) = {\rm cos}^2(\pi \cdot {t}/{T_{\rm P}}) = 0.5+ 0.5\cdot {\rm cos}(2\pi \cdot {t}/{T_{\rm P}})\hspace{0.05cm}.$$ Nach Zeitdiskretisierung mit $ν = t/T_{\rm A}$ und $T_{\rm P}/T_{\rm A} = N = 32$ erhält man für das zeitdiskrete Fenster: $$w(\nu) = w(\nu \cdot T_{\rm A}) = 0.5+ 0.5\cdot {\rm cos}(2\pi \cdot {\nu}/{N})\hspace{0.8cm} \Rightarrow \hspace{0.3cm}w(\nu = 0) \hspace{0.15 cm}\underline{= 1},$$ $$w(\nu = 1) = 0.5+ 0.5\cdot {\rm cos}( \frac{\pi}{16})\hspace{0.15 cm}\underline{ = 0.99}, \hspace{0.35cm}w(\nu = -8)=0.5+ 0.5\cdot {\rm cos}( \frac{-\pi}{2}) \hspace{0.15 cm}\underline{= 0.5}\hspace{0.05cm}.$$

(2)  Die periodische Fortsetzung von $w(t)$ entsprechend der Periodendauer $T_{\rm P}$ liefert ein (periodisches) Signal mit einem Gleich– und einem Cosinusanteil. Daraus folgt mit $f_{\rm A} = 1/T_{\rm P}$: $${\rm P}\{w(t)\} = 0.5+0.5\cdot {\rm cos}(2\pi \cdot f_{\rm A} \cdot t) \hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm}0.5\cdot {\rm \delta}(f) + 0.25\cdot {\rm \delta}(f \pm f_{\rm A}))\hspace{0.05cm}.$$ Das zeitbegrenzte Signal $w(t)$ ergibt sich aus ${\rm P}\{w(t)\}$ durch Multiplikation mit einem Rechteck der Amplitude $1$ und der Dauer $T_{\rm P}$. Dessen Spektrum $W(f)$ erhält man somit aus der Faltung der obigen Spektralfunktion mit der Funktion $T_{\rm P} · {\rm si}(π \cdot f \cdot T_{\rm P}) = 1/f_{\rm A} · {\rm si}(π \cdot f/f_{\rm A})$: $$w(t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, W(f) = \frac{0.5}{f_{\rm A}}\cdot {\rm si}( \frac{\pi f}{f_{\rm A}})+ \frac{0.25}{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f-f_{\rm A}}{f_{\rm A}})+ \frac{0.25}{f_{\rm A}}\cdot {\rm si}(\pi \cdot \frac{f+f_{\rm A}}{f_{\rm A}})\hspace{0.05cm}.$$ Diese Spektralfunktion ist gerade und für alle Frequenzen $f$ auch reell. Der Spektralwert bei der Frequenz $f = 0$ ergibt die Fensterfläche: $$W(f=0) = \frac{0.5}{f_{\rm A}}= \int_{-\infty}^{+\infty}w(t)\hspace{0.05cm}{\rm d}t\hspace{0.05cm}.$$ Richtig sind somit die Lösungsvorschläge 2 und 3.

(3)  Das Ergebnis der Teilaufgabe (2) zeigt weiter, dass $W(f = ±fA) = W(0)/2$ ist. Aufgrund des monotonen Verlaufs im Bereich $|f| < ff_{\rm A}$ ist die Betragsfunktion $|W(f)|$ genau bei $± f_{\rm A}$ zum ersten Mal auf die Hälfte des Maximums abgefallen. Damit gilt $B_{\rm 6\hspace{0.05cm}dB}\hspace{-0.05cm}/\hspace{-0.05cm}f_{\rm A} \;\underline{=2}$.

(4)  Der größte Spektralbetrag außerhalb der Hauptkeule tritt bei den Frequenzen $f = ±2.5 f_{\rm A}$ auf. Mit dem Ergebnis der Teilaufgabe (2) gilt: $$W(f = 2.5 \cdot f_{\rm A}) = \frac{0.5}{f_{\rm A}}\cdot {\rm si}(2.5 \pi ) +\frac{0.25}{f_{\rm A}}\cdot {\rm si}(1.5 \pi )+\frac{0.25}{f_{\rm A}}\cdot {\rm si}(3.5 \pi )= \frac{0.25}{\pi \cdot f_{\rm A}}\left[ \frac{2}{2.5}-\frac{1}{1.5}-\frac{1}{3.5}\right] \approx -\frac{0.0121}{ f_{\rm A}}\hspace{0.05cm}.$$ Damit erhält man für den minimalen Abstand zwischen Hauptkeule und Seitenkeulen: $$A_{\rm H/S} = 20 \cdot {\rm lg}\hspace{0.15cm} \frac{|W(0)|}{|W(2.5 \cdot f_{\rm A})|} = 20 \cdot {\rm lg}\hspace{0.15cm} \frac{0.5}{0.0121}\hspace{0.15 cm}\underline{\approx 32.3\,\,{\rm dB}}\hspace{0.05cm}.$$