Exercise 3.3Z: Moments for Triangular PDF

Wir betrachten in dieser Aufgabe zwei Zufallssignale $x(t)$ und $y(t)$ mit jeweils dreieckförmiger WDF, nämlich die

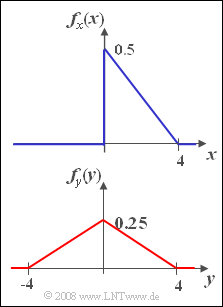
einseitige Dreieck-WDFgemäß der oberen Grafik:

$$f_x(x)=\left\{ \begin{array}{*{4}{c}} 0.5 \cdot (1-{ x}/{\rm 4}) & \rm f\ddot{u}r\hspace{0.1cm}{\rm 0 \le {\it x} \le 4},\\\rm 0 & \rm sonst. \end{array} \right.$$

zweiseitige Dreieck-WDF gemäß der unteren Grafik:

$$ f_y(y)=\left\{ \begin{array}{*{4}{c}} 0.25 \cdot (1-{ |y|}/{\rm 4}) & \rm f\ddot{u}r\hspace{0.1cm}{ -4 \le {\it y} \le \rm 4},\\\rm 0 & \rm sonst. \end{array} \right.$$

Berücksichtigen Sie zur Lösung dieser Aufgabe die Gleichung für die Zentralmomente: $$\mu_k=\sum\limits_{\kappa = \rm 0}^{\it k}\left({k} \atop {\kappa}\right)\cdot m_k\cdot(-m_{\rm 1})^{k - \kappa}.$$

Im Einzelnen ergeben sich mit dieser Gleichung folgende Ergebnisse: $$\mu_{\rm 1}=0,\hspace{0.5cm}\mu_{\rm 2}=\it m_{\rm 2}-\it m_{\rm 1}^{\rm 2},\hspace{0.5cm}\mu_{\rm 3}=\it m_{\rm 3}-\rm 3\cdot\it m_{\rm 2}\cdot \it m_{\rm 1} {\rm +}\rm 2\cdot\it m_{\rm 1}^{\rm 3},$$ $$\mu_{\rm 4}=\it m_{\rm 4}-\rm 4\cdot\it m_{\rm 3}\cdot \it m_{\rm 1}\rm +6\cdot\it m_{\rm 2}\cdot\it m_{\rm 1}^{\rm 2}-\rm 3\cdot\it m_{\rm 1}^{\rm 4}.$$

Aus den Zentralmomenten höherer Ordnung kann man unter anderem ableiten:

die Charliersche Schiefe $S = {\mu_3}/{\sigma^3}\hspace{0.05cm},$

die Kurtosis $K = {\mu_4}/{\sigma^4}\hspace{0.05cm}.$

Hinweise:

Die Aufgabe gehört zum Kapitel Erwartungswerte und Momente.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

$m_x \ =$

$\sigma_x\ =$

$S_x \ =$

	Alle Momente mit ungeradzahligem $k$ sind $m_k =0$.
	Alle Momente mit geradzahligem $k$ sind $m_k =0$.
	Alle Momente $m_k$ mit geradzahligem $k$ sind wie in der Teilaufgabe (1) berechnet.
	Die Zentralmomente $\mu_k$ sind gleich den Momenten $m_k$>.

$\sigma_y \ =$

$K_y \ =$

Musterlösung

Solution

1. Für das Moment k-ter Ordnung gilt nach den Gleichungen von Kapitel 3.3:

$$m_k=\rm \frac{\rm 1} {\rm 2}\cdot \int_{\rm 0}^{\rm 4}\it x^k\cdot (\rm 1-\frac{\it x}{\rm 4})\it \hspace{0.1cm}{\rm d}x.$$

Dies führt zu dem Ergebnis:

$$m_k=\frac{x^{\it k+\rm 1}}{\rm 2\cdot (\it k+\rm 1)}\Bigg|_{\rm 0}^{\rm 4}-\frac{x^{\it k+\rm 2}}{\rm 8\cdot (\it k+\rm 2)}\Bigg|_{\rm 0}^{\rm 4}=\frac{\rm 2\cdot \rm 4^{\it k}}{(\it k+\rm 1)\cdot (\it k+\rm 2)}.$$

Daraus erhält man für den linearen Mittelwert (k = 1):

$$m_x=\rm {4}/{3}\hspace{0.15cm}\underline{=1.333}.$$

2. Der quadratische Mittelwert (k = 2) beträgt m₂ = 8/3. Daraus folgt mit dem Satz von Steiner:

$$\sigma_x^{\rm 2}=\rm\frac{8}{3}-\Bigg(\frac{4}{3}\Bigg)^2=\rm \frac{8}{9}\hspace{0.5cm}\Rightarrow\hspace{0.5cm}\it \sigma_x\hspace{0.15cm}\underline{\approx \rm 0.943}.$$

3. Mit m₁ = 4/3, m₂ = 8/3 und m₃ = 32/5 erhält man mit der angegebenen Gleichung für das Zentralmoment dritter Ordnung: μ₃ = 64/135 ≈ 0.474. Daraus folgt für die Charliersche Schiefe:

$$S_x=\rm \frac{64/135}{\Big(\sqrt {8/9}\Big)^3}=\frac{\sqrt{8}}{5}\hspace{0.15cm}\underline{\approx 0.566}.$$

Aufgrund der unsymmetrischen WDF ist S_x ≠ 0.

4. Bei symmetrischer WDF sind alle ungeraden Momente 0, unter anderem auch der Mittelwert m_y. Deshalb gibt es hinsichtlich der Zufallsgröße y keinen Unterschied zwischen den Momenten m_k und den Zentralmomenten μ_k.

Die Momente m_k mit geradzahligem k sind für die Zufallsgrößen x und y gleich. Offensichtlich wird dies an den Zeitmittelwerten. Da x²(t) = y²(t) ist, sind für k = 2n auch die Momente gleich:

$$m_k=m_{2 n}=...\int [x^2(t)]^n \hspace{0.1cm}{\rm d} x=...\int [y^2(t)]^n \hspace{0.1cm}{\rm d} y.$$

Richtig sind somit die Lösungsvorschläge 1, 3 und 4.

5. Mit dem Ergebnis aus b) gilt:

$$m_2=\mu_{\rm 2}=\sigma_y^2=\rm \frac{8}{3} = 2.667\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_y\hspace{0.15cm}\underline{=1.633}.$$

6. Das Zentralmoment vierter Ordnung ist bei symmetrischer WDF gleich dem Moment m₄. Aus der im Punkt a) berechneten allgemeinen Gleichung erhält man

μ₄ = 256/15. Daraus folgt für die Kurtosis:

$$K_y=\frac{\mu_{\rm 4}}{\sigma_y^{\rm 4}}=\rm \frac{256/15}{(8/3)^2}\hspace{0.15cm}\underline{=2.4}.$$

Dieser Zahlenwert gilt für die Dreieck-WDF allgemein und liegt zwischen den Kurtosiswerten von Gleichverteilung (K = 1.8) und Gaußverteilung (K = 3). Dies ist eine qualitative Bewertung der Tatsache, dass hier die Ausläufer ausgeprägter sind als bei einer gleichverteilten Zufallsgröße, aber aufgrund der Begrenzung weniger stark als bei Gaußschen Größen.

Anschließend soll noch nachgewiesen werden, dass auch die unsymmetrische Dreieck-WDF f_x(x) entsprechend der oberen Skizze auf dem Angabenblatt die gleiche Kurtosis besitzt:

$$\mu_{\rm 4} = \it m_{\rm 4}-\rm 4\cdot\it m_{\rm 3}\cdot \it m_{\rm 1}+\rm 6\cdot\it m_{\rm 2}\cdot\it m_{\rm 1}^{\rm 2}-\rm 3\cdot\it m_{\rm 1}^{\rm 4}= \\ = \frac{256}{15} - 4 \cdot \frac{32}{5}\cdot \frac{4}{3} + 6 \cdot \frac{8}{3}\cdot \left(\frac{4}{3}\right)^2 -3 \cdot \left(\frac{4}{3}\right)^4 =\frac{256}{15 \cdot 9}$$

Mit dem Ergebnis der Teilaufgabe (c) ⇒ σ_x² = 8/9 folgt daraus:

$$ K_x = \frac{{256}/(15 \cdot 9)}{8/9 \cdot 8/9} = 2.4.$$