Exercise 5.5Z: Complexity of the FFT
Der FFT–Algorithmus realisiert eine Diskrete Fouriertransformation mit dem kleinstmöglichen Rechenaufwand, wenn der Parameter N eine Zweierpotenz ist. Im einzelnen sind zur Durchführung einer FFT folgende Rechenschritte notwendig:
- Die FFT geschieht in ld N Stufen, wobei in jeder Stufe die genau gleiche Anzahl an Rechenoperationen durchzuführen ist. „ld” steht hier als Abkürzung für den Logarithmus zur Basis 2.
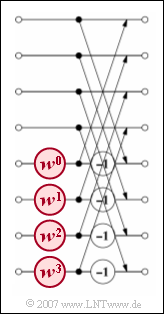
- Die Grafik zeigt die dritte und letzte Stufe für das Beispiel N = 8. Man erkennt, dass in dieser und auch den anderen Stufen jeweils N/2 Basisoperationen durchzuführen sind.
- In jeder Basisoperation, die man häufig auch als Butterfly bezeichnet, werden aus den beiden komplexen Eingangsgrößen $E_1$ und $E_2$ zwei komplexe Ausgänge berechnet:
$$ A_1 = E_1 + E_2 \cdot w^{\hspace{0.04cm}\mu}, $$ $$ A_2 = E_1 - E_2 \cdot w^{\hspace{0.04cm} \mu}\hspace{0.05cm}.$$
- Hierbei bezeichnet w = exp(–j · 2π/N) den komplexen Drehfaktor. Für das Beispiel N = 8 hat dieser folgenden Wert:
$w = {\rm e}^{-{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \pi/4} = \cos(45^\circ) - {\rm j} \cdot \sin(45^\circ)\hspace{0.05cm}.$
- Der Exponent $\mu$ dieses komplexen Drehfaktors kann alle ganzzahligen Werte zwischen 0 und N/2 –1 annehmen. Für N = 8 gilt:
$w^0 = 1,\hspace{0.2cm}w^1 = \frac{1}{\sqrt{2}}- {\rm j} \cdot\frac{1}{\sqrt{2}},\hspace{0.2cm}w^2 = - {\rm j},\hspace{0.2cm}w^3 = -\frac{1}{\sqrt{2}}- {\rm j} \cdot\frac{1}{\sqrt{2}} \hspace{0.05cm}.$
Mit dieser Aufgabe sollen die für die FFT erforderliche Anzahl von Rechenoperationen $(O_{FFT})$ ermittelt und mit dem für die DFT angebbaren Wert $O_{DFT}$ ≈ 8N$ ^2$ verglichen werden.
Zu beachten ist:
- Sinnvollerweise werden die Potenzen von w vor dem eigentlichen Algorithmus berechnet und in einer Lookup–Tabelle abgelegt. Die hierfür notwendigen Operationen sollen deshalb unberücksichtigt bleiben.
- Die Bitumkehroperation – eine Umsortierung, die vor der ersten Stufe durchzuführen ist – soll bei dieser Abschätzung ebenfalls nicht berücksichtigt werden.
Fragebogen
Musterlösung