Exercise 4.4: Conventional Entropy and Differential Entropy
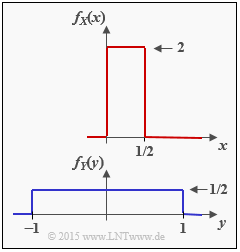
Wir betrachten die zwei wertkontinuierlichen Zufallsgrößen X und Y mit den Wahrscheinlichkeitsdichtefunktionen fX(x) und fY(y). Für diese Zufallsgrößen kann man
- die herkömmlichen Entropien H(X), H(Y) nicht angeben,
- jedoch aber die differentiellen Entropien h(X) und h(Y).
Wir betrachten außerdem zwei wertdiskrete Zufallsgrößen:
- ZX,M ergibt sich durch (geeignete) Quantisierung der Zufallsgröße X mit der Quantisierungsstufenzahl M ⇒ Quantisierungsintervallbreite Δ = 0.5/M.
- Die Zufallsgröße ZY,M ergibt sich nach Quantisierung der wertkontinuierlichen Zufallsgröße Y mit der Quantisierungsstufenzahl M ⇒ Quantisierungsintervallbreite Δ = 2/M.
Die Wahrscheinlichkeitsdichtefunktionen dieser diskreten Zufallsgrößen setzen sich jeweils aus M Diracfunktionen zusammen, deren Impulsgewichte durch die Intervallflächen der zugehörigen wertkontinuierlichen Zufallsgrößen gegeben sind. Daraus lassen sich die Entropien H(ZX,M) und H(ZY,M) in herkömmlicher Weise (entsprechend Kapitel 3) bestimmen.
Im Theorieteil wurde auch eine Näherung angegeben. Beispielsweise gilt: $$H(Z_{X, \hspace{0.05cm}M}) \approx -{\rm log}_2 \hspace{0.1cm} ({\it \Delta}) + h(X)\hspace{0.05cm}. $$ Sie werden im Laufe der Aufgabe feststellen, dass bei rechteckförmiger WDF ⇒ Gleichverteilung diese „Näherung” genau das gleiche Ergebnis liefert wie die direkte Berechnung. Aber im allgemeinen Fall – zum Beispiel bei dreieckförmiger WDF – stellt obige Gleichung tatsächlich nur eine Näherung dar, die erst im Grenzfall Δ → 0 mit der tatsächlichen Entropie H(ZX,M) übereinstimmt.
Hinweis: Die Aufgabe gehört zum Themengebiet von Kapitel 4.1
Fragebogen
Musterlösung