Aufgaben:Aufgabe 2.13Z: Kombination BWT & ''Move-to-Front''

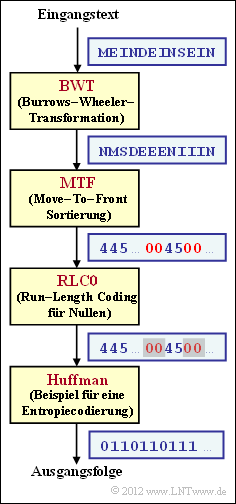
Schema für die Burrows–Wheeler–Datenkomprimierung

Wir beziehen uns auf die Theorieseite Anwendungsszenario für_die_Burrows-Wheeler-Transformation und betrachten das rechts skizzierte Codiersystem, bestehend aus den Blöcken.

Burrows–Wheeler–Transformation (BWT) gemäß der Beschreibung in Aufgabe 2.13; die beiden Zeichenmengen am Ein– und Ausgang des BWT sind gleich: $\{$D, E, I, M, N, S$\}$;
Move–to–Front (MTF), ein Sortieralgorithmus, der eine gleich lange Zeichenfolge (im Beispiel $N = 12$), aber mit anderem Alphabet $\{$0, 1, 2, 3, 4, 5$\}$ ausgibt;
RLC0 – eine Lauflängencodierung speziell für die nach BWT und MTF (möglichst) häufige Null; alle anderen Indizes werden durch „RLC0” nicht verändert;
Huffman gemäß der Beschreibung im Kapitel Entropiecodierung nach Huffman; häufige Zeichen werden durch kurze Binärfolgen dargestellt, seltene durch lange.

Der MTF–Algorithmus lässt sich wie folgt beschreiben:

Bei $M = 6$ Eingangssymbolen ist die Ausgangsfolge des MTF eine Aneinanderreihung von Indizes aus der Menge I$ = \{$0, 1, 2, 3, 4, 5$\}$.
Vor Beginn des eigentlichen MTF–Algorithmus werden die möglichen Eingangssymbole lexikografisch sortiert und den folgenden Indizes zugeordnet:

D → 0, E → 1, I → 2, M → 3, N → 4, S → 5.

Der MTF–Eingabestring sei hier NMSDEEENIIIN. Dies war das BWT–Ergebnis in der Aufgabe 2.13. Das erste N wird gemäß Voreinstellung mit I = 4 dargestellt.
Anschließend wird das N in der Sortierung an den Anfang gestellt, so dass nach dem Codierschritt $i = 1$ folgende Zuordnung gilt:

N → 0, D → 1, E → 2, I → 3, M → 4, S → 5.

In gleicher Weise fährt man fort, bis der gesamte Eingangstext abgearbeitet ist. Steht ein Zeichen bereits an Position 0, so ist keine Neusortierung erforderlich.

Hinweise:

Die Aufgabe gehört zum Kapitel Weitere Quellencodierverfahren.
Insbesondere wird Bezug genommen auf die Seite Burrows–Wheeler–Transformation.
Informationen zum Huffman–Code finden Sie im Kapitel Entropiecodierung nach Huffman. Für die Lösung dieser Aufgabe sind diese Informationen aber nicht erforderlich.

Fragebogen

Musterlösung

Solution

1. Die Grafik auf der Angabenseite zeigt, dass die Lösungsvorschläge 1 und 2 richtig sind und der Vorschlag 3 falsch ist. E und I treten zwar gruppiert auf, aber nicht die N–Zeichen.

2. Richtig sind die Lösungsvorschläge 2 und 3. Die Eingangsfolge wird Zeichen für Zeichen abgearbeitet. Auch die Ausgangsfolge hat somit die Länge N = 12.

Tatsächlich wird die Eingangsmenge {D, E, I, N, M, S} in die Ausgangsmenge {0, 1, 2, 3, 4, 5} gewandelt. Allerdings nicht durch einfaches Mapping, sondern durch einen Algorithmus, der nachfolgend skizziert wird.

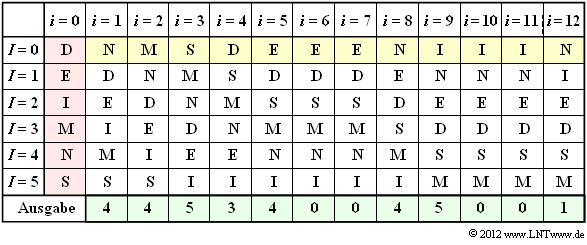
3. Die folgende Tabelle zeigt den MTF–Algorithmus. Der Schritt i = 0 (rote Hinterlegung) gibt die Vorbelegung an. Die Eingabe der MTF ist gelb hinterlegt, die Ausgabe grün.

Im Schritt i = 1 wird das Eingangszeichen N entsprechend der Spalte i = 0 durch den Index I = 4 dargestellt. Anschließend wird N nach vorne sortiert, während die Reihenfolge der anderen Zeichen gleich bleibt.

Das Eingangszeichen M im zweiten Schritt erhält entsprechend der Spalte i = 1 ebenfalls den Index I = 4. In gleicher Weise macht man weiter bis zum 12. Zeichen N, dem der Index I = 1 zugeordnet wird.

Richtig ist Lösungsvorschlag 2. Man erkennt aus obiger Tabelle weiter, dass zu den Zeitpunkten i = 6, i = 7, i = 10 und i = 11 der Ausgabeindex jeweils I = 0 ist.

4. Richtig sind die Aussagen 1 und 2. Die Vorverarbeitungsschritte BWT und MTF haben lediglich die Aufgabe, möglichst viele Nullen zu generieren.

5. Alle Aussagen sind richtig. Nähere Angaben zum Huffman–Algorithmus finden Sie im Kapitel 2.3.

	Die Eingangszeichenmenge ist $\{$D, E, I, M, N, S$\}$.
	Die Ausgangszeichenmenge ist $\{$D, E, I, M, N, S$\}$.
	In der Ausgangsfolge treten alle $M = 6$ Zeichen gruppiert auf.

	Die Ausgangszeichenmenge ist $\{$D, E, I, M, N, S$\}$.
	Die Ausgangszeichenmenge ist $\{$0, 1, 2, 3, 4, 5$\}$.
	Die MTF–Ausgangsfolge hat die Länge $N = 12$.

	Der Eingangswert 0 erfährt eine Sonderbehandlung.
	Je häufiger eine 0 auftritt, um so effektiver ist dieser Block.
	Am besten wäre Pr(0) ≈ Pr(1) ≈ ... ≈ Pr(5).

	Die Ausgangsfolge ist binär.
	Er bewirkt eine möglichst kleine mittlere Codewortlänge.
	Die Dimensionierung richtet sich nach den anderen Blöcken.

	230000100405,
	445340045001,
	543120345123.