Im Mittelpunkt dieses dritten Kapitels steht die Transinformation $I(X; Y)$ zwischen zwei Zufallsgrößen $X$ und $Y$, wofür auch andere Begriffe wie Mutual Information oder gegenseitige Entropie üblich sind. Bei statistischer Abhängigkeit ist $I(X; Y)$ kleiner als die Einzelentropien $H(X)$ bzw. $H(Y)$. Beispielsweise wird die Unsicherheit hinsichtlich der Zufallsgröße $X$ ⇒ Entropie $H(X)$ durch die Kenntnis von $Y$ vermindert, und zwar um den Betrag $H(X\hspace{0.03cm}|\hspace{0.03cm}Y)$ ⇒ bedingte Entropie von $X$, falls $Y$ bekannt ist. Der verbleibende Rest ist die Transinformation $I(X; Y)$. Gleichzeitig gilt aber auch $I(X; Y) = H(Y) - H(Y\hspace{0.03cm}|\hspace{0.03cm}X)$. Das Semikolon weist auf die Gleichberechtigung der beiden betrachteten Zufallsgrößen $X$ und $Y$ hin.
Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im Versuch „Wertdiskrete Informationstheorie” des Praktikums „Simulation Digitaler Übertragungssysteme ”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf
- dem Windows-Programm WDIT ⇒ Link verweist auf die ZIP-Version des Programms; und
- der zugehörigen Praktikumsanleitung ⇒ Link verweist auf die PDF-Version.
Der erste Abschnitt „Allgemeine Beschreibung” ist wie folgt gegliedert:
Contents
Einführungsbeispiel zur statistischen Abhängigkeit von Zufallsgrößen
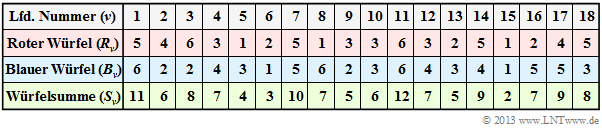
Wir gehen vom Experiment „Würfeln mit zwei Würfeln” aus, wobei beide Würfel (an der Farbe) unterscheidbar sind. Die untere Tabelle zeigt als Ergebnis die ersten $N = 18$ Wurfpaare dieses exemplarischen Zufallsexperiments.
Hinweis: Entsprechend der im nachfolgendem Abschnitt erklärten Nomenklatur sind hier $R_ν$, $B_ν$ und $S_ν$ als Zufallsgrößen zu verstehen. Die Zufallsgröße $R_3 = \{1, 2, 3, 4, 5, 6\}$ gibt beispielsweise die Augenzahl des roten Würfels beim dritten Wurf als Wahrscheinlichkeitsereignis an. Die Angabe $R_3 = 6$ sagt aus, dass bei der dokumentierten Realisierung der rote Würfel im dritten Wurf eine „6” gezeigt hat.
- In Zeile 2 sind die Augenzahlen des roten Würfels ($R$) angegeben. Der Mittelwert dieser begrenzten Folge $〈R_1, ... , R_{18}〉$ ist mit 3.39 etwas kleiner als der Erwartungswert ${\rm E}[R] = 3.5$.
- Die Zeile 3 zeigt die Augenzahlen des blauen Würfels ($B$). Die Folge $〈B_1, ... , B_{18}〉$ hat mit $3.61$ einen etwas größeren Mittelwert als die unbegrenzte Folge ⇒ ${\rm E}[B] = 3.5$.
- Zeile 4 beinhaltet die Summe $S_ν = R_ν + B_ν$. Der Mittelwert der Folge $〈S_1, ... , S_{18}〉$ ist $3.39 + 3.61 = 7$. Dieser ist hier (zufällig) gleich dem Erwartungswert $\text{E}[S] = \text{E}[R] + \text{E}[B]$.
Nun stellt sich die Frage, zwischen welchen Zufallsgrößen es statistische Abhängigkeiten gibt:
- Setzt man faire Würfel voraus, so bestehen zwischen den Folgen $〈R〉$ und $〈B〉$ – ob begrenzt oder unbegrenzt – keine statistischen Bindungen: Auch wenn man $R_ν$ kennt, sind für $B_ν$ weiterhin alle möglichen Augenzahlen $1$, ... , $6$ gleichwahrscheinlich.
- Kennt man aber $S_ν$, so sind sowohl Aussagen über $R_ν$ als auch über $B_ν$ möglich. Aus $S_{11} = 12$ (siehe obige Tabelle) folgt direkt $R_{11} = B_{11} = 6$ und die Summe $S_{15} = 2$ zweier Würfel ist nur mit zwei Einsen möglich. Solche Abhängigkeiten bezeichnet man als deterministisch.
- Aus $S_7 = 10$ lassen sich zumindest Bereiche für $R_7$ und $B_7$ angeben: $R_7 ≥ 4, \ B_7 ≥ 4$. Möglich sind dann nur die drei Wertepaare $(R_7 = 4) ∩ (B_7 = 6)$, $(R_7 = 5) ∩ (B_7 = 5)$ sowie $(R_7 = 6) ∩ (B_7 = 4)$. Hier besteht zwar kein deterministischer Zusammenhang zwischen den Zufallsgrößen $S_ν$ und $R_ν$ (bzw. $B_ν$), aber eine so genannte statistische Abhängigkeit.
- Solche statistische Abhängigkeiten gibt es für alle $S_ν ∈ \{3, 4, 5, 6, 8, 9, 10, 11\}$. Ist dagegen die Summe $S_ν = 7$, so kann daraus nicht auf $R_ν$ und $B_ν$ zurückgeschlossen werden. Für beide Würfel sind dann alle möglichen Augenzahlen $1$, ... , $6$ gleichwahrscheinlich. In diesem Fall bestehen auch keine statistischen Bindungen zwischen $S_ν$ und $R_ν$ bzw. zwischen $S_ν$ und $B_ν$.
Voraussetzungen und Nomenklatur
Wir betrachten im gesamten Kapitel wertdiskrete Zufallsgrößen der Form $X = \{ x_1, x_2, \hspace{0.05cm}... \hspace{0.15cm}, x_{\mu},\hspace{0.05cm}$ ... $\hspace{0.15cm}, x_M \} \hspace{0.05cm},$ und verwenden folgende Nomenklatur:
- Die Zufallsgröße selbst wird stets mit einem Großbuchstaben bezeichnet, und der Kleinbuchstabe $x$ weist auf eine mögliche Realisierung der Zufallsgröße $X$ hin.
- Alle Realisierungen $x_μ$ (mit $μ = 1$, ... , $M$) sind reellwertig. $M$ gibt den Symbolumfang (englisch: Symbol Set Size) von $X$ an. Anstelle von $M$ verwenden wir manchmal auch $|X|$.
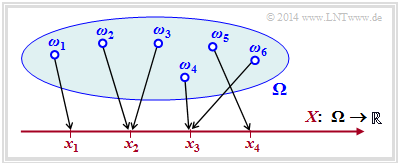
Die Zufallsgröße $X$ kann zum Beispiel durch die Transformation $\Omega → X$ entstanden sein, wobei $\Omega$ für den Wahrscheinlichkeitsraum eines Zufallsexperiments steht. Die nachfolgende Grafik verdeutlicht eine solche Transformation:
- $${\it \Omega} = \{ \omega_1, \omega_2, \omega_3, ... \hspace{0.15cm} \} \hspace{0.25cm} \longmapsto \hspace{0.25cm} X = \{ x_1, x_2, x_3, x_4\} \subset \cal{R}\hspace{0.05cm}.$$
Jedes Zufallsereignis $ω_i ∈ Ω$ wird eindeutig einem reellen Zahlenwert $x_μ ∈ X ⊂ ℝ$ zugeordnet. Im betrachteten Beispiel gilt für die Laufvariable $1 ≤ μ ≤ 4$, das heißt, der Symbolumfang beträgt $M = |X| = 4$.
Die Abbildung ist aber nicht eineindeutig: Die Realisierung $x_3 ∈ X$ könnte sich im Beispiel aus dem Elementarereignis $ω_4$ ergeben haben, aber auch aus $ω_6$ (oder aus einem anderen der unendlich vielen, in der Grafik nicht eingezeichneten Elementarereignisse $ω_i$).
Oft verzichtet man auf die Indizierung sowohl der Elementarereignisse $ω_i$ als auch der Realisierungen $x_μ$. Damit ergeben sich beispielsweise folgende Kurzschreibweisen:
- $$ \{ X = x \} \hspace{0.05cm} \equiv \hspace{0.05cm} \{ \omega \in {\it \Omega} : \hspace{0.4cm} X(\omega) = x \} \hspace{0.05cm},$$
- $$ \{ X \le x \} \hspace{0.05cm} \equiv \hspace{0.05cm} \{ \omega \in {\it \Omega} : \hspace{0.4cm} X(\omega) \le x \} \hspace{0.05cm}.$$
Mit dieser Vereinbarung gilt für die Wahrscheinlichkeiten der diskreten Zufallsgröße $X$:
- $${\rm Pr}( X = x_{\mu}) = \hspace{-0.2cm} \sum_{\omega \hspace{0.1cm} \in \{ X = x_{\mu} \}} \hspace{-0.2cm}{\rm Pr} \left ( \{ \omega \} \right ) \hspace{0.05cm}.$$
Wahrscheinlichkeitsfunktion und Wahrscheinlichkeitsdichtefunktion
Definition: Fasst man die $M$ Wahrscheinlichkeiten einer diskreten Zufallsgröße $X$ ⇒ ${\rm Pr}( X = x_{\mu})$ ähnlich wie bei einem Vektor zusammen, so kommt man zur Wahrscheinlichkeitsfunktion (englisch: Probability Mass Function, PMF):
- $$P_X(X) = \big [ \hspace{0.02cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}... \hspace{0.15cm}, P_X(x_{\mu}),\hspace{0.05cm} ...\hspace{0.15cm}, P_X(x_M) \hspace{0.02cm} \big ] \hspace{0.05cm}.$$
Im Buch„Stochastische Signaltheorie” haben wir mit der Wahrscheinlichkeitsdichtefunktion (WDF, englisch: Probability Density Function, PDF) eine ähnliche Beschreibungsgröße definiert und diese mit $f_X(x)$ bezeichnet.
Zu beachten ist aber:
- Die PDF eignet sich eher zur Charakterisierung kontinuierlicher Zufallsgrößen, wie zum Beispiel bei einer Gaußverteilung oder einer Gleichverteilung. Erst durch die Verwendung von Diracfunktionen wird die PDF auch für diskrete Zufallsgrößen anwendbar.
- Die PMF liefert weniger Information über die Zufallsgröße als die PDF und kann zudem nur für diskrete Größen angegeben werden. Für die wertdiskrete Informationstheorie ist die PMF allerdings ausreichend.
{{GraueBox|
TEXT=Beispiel 1: Wir betrachten eine Wahrscheinlichkeitsdichtefunktion (abgekürzt WDF bzw. PDF) ohne großen Praxisbezug:
- $$f_X(x) = 0.2 \cdot (x+2) + 0.3 \cdot (x-1.5)+0.5 \cdot (x-{\rm \pi}) \hspace{0.05cm}. $$
Für die diskrete Zufallsgröße gilt somit $x ∈ X = \{–2, +1.5, +\pi \} $ ⇒ Symbolumfang $M = 3$, und die Wahrscheinlichkeitsfunktion (PMF) lautet:
- $$P_X(X) = \big [ \hspace{0.1cm}0.2\hspace{0.05cm}, 0.3\hspace{0.05cm}, 0.5 \hspace{0.1cm} \big] \hspace{0.05cm}. $$
Man erkennt:
- Die PMF liefert nur Informationen über die Wahrscheinlichkeiten $\text{Pr}(x_1)$, $\text{Pr}(x_2)$, $\text{Pr}(x_3)$. Aus der PDF sind dagegen auch die möglichen Realisierungen $x_1$, $x_2$, $x_3$ der Zufallsgröße $X$ ablesbar.
- Die einzige Voraussetzung für die Zufallsgröße ist, dass sie reellwertig ist. Die möglichen Werte $x_μ$ müssen weder positiv, ganzzahlig, äquidistant noch rational sein. }}
Wahrscheinlichkeitsfunktion und Entropie
In der wertdiskreten Informationstheorie genügt im Gegensatz zu übertragungstechnischen Problemen schon die Kenntnis der Wahrscheinlichkeitsfunktion $P_X(X)$, zum Beispiel zur Berechnung der Entropie.
Definition: Die Entropie einer diskreten Zufallsgröße $X$ – also deren Unsicherheit für einen Beobachter – kann man mit der Wahrscheinlichkeitsfunktion $P_X(X)$ wie folgt darstellen:
- $$H(X) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_X(X)}\right ] \hspace{0.05cm}=\hspace{0.05cm} -{\rm E} \left [ {\rm log} \hspace{0.1cm} {P_X(X)}\right ] \hspace{0.05cm}=\hspace{0.05cm} \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}=\hspace{0.05cm} - \sum_{\mu = 1}^{M} P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} {P_X(x_{\mu})} \hspace{0.05cm}.$$
Beispielsweise erhält man
- für $P_X(X) = \big [\hspace{0.02cm}0.2, 0.3, 0.5 \hspace{0.02cm}\big ]$:
- $$H(X) = 0.2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.2} + 0.3 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.3} +0.5 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{0.5} \approx 1.485\,{\rm bit}\hspace{0.05cm},$$
- für $P_X(X) = \big [\hspace{0.02cm}1/3, 1/3, 1/3\hspace{0.02cm}\big ]$:
- $$H(X) = 3 \cdot 1/3 \cdot {\rm log}_2 \hspace{0.1cm} (3) = {\rm log}_2 \hspace{0.1cm} (3) \approx 1.585\,{\rm bit}\hspace{0.05cm}.$$
Das zweite Beispiel liefert das Maximum der Entropiefunktion für den Symbolumfang $M = 3$. Für ein allgemeines $M$ lässt sich dieses Ergebnis beispielsweise wie folgt herleiten – siehe [Meck][1]:
- $$H(X) = -{\rm E} \left [ {\rm log} \hspace{0.1cm} {P_X(X)}\right ] \hspace{0.2cm} \le \hspace{0.2cm}- {\rm log} \left [ {\rm E} \hspace{0.1cm} \left [{P_X(X)}\right ] \right ] \hspace{0.05cm}.$$
Diese Abschätzung (Jensens's Ungleichung) ist zulässig, da der Logarithmus eine konkave Funktion ist. Entsprechend Aufgabe 3.2 gilt:
$$-{\rm E} \left [ {P_X(X)}\right ] \hspace{0.1cm} \le \hspace{0.1cm} M \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H(X) \le {\rm log} \hspace{0.1cm} (M) \hspace{0.05cm}.$$
Das Gleichheitszeichen ergibt sich nach der oberen Rechnung für gleiche Wahrscheinlichkeiten, also für $P_X(x_μ) = {1}/{M}$ für alle $μ$. In der Aufgabe 3.3 soll der gleiche Sachverhalt unter Verwendung der Abschätzung
$${\rm ln} \hspace{0.1cm} (x) \le x-1$$
nachgewiesen werden. Das Gleichheitszeichen gilt hier nur für $x = 1$.
Ist eine der $M$ Wahrscheinlichkeiten $P_X(x_μ)$ der Wahrscheinlichkeitsfunktion gleich 0, so lässt sich für die Entropie eine engere Schranke angeben:
- $$H(X) \le {\rm log} \hspace{0.1cm} (M-1) \hspace{0.05cm}.$$
Für das folgende Beispiel und die nächsten Seiten vereinbaren wir die folgende Nomenklatur:
- Die Entropie $H(X)$ bezieht sich stets auf die tatsächliche Wahrscheinlichkeitsfunktion $P_X(X)$ der diskreten Zufallsgröße. Experimentell erhält man diese Größen erst nach $N → ∞$ Versuchen.
- Ermittelt man die Wahrscheinlichkeitsfunktion aus einer endlichen Zufallsfolge, so bezeichnen wir diese mit $Q_X(X)$ und die daraus resultierende Entropie versehen wir mit dem Zusatz „$N =$ ...”.
- Diese Entropie–Näherung basiert nicht auf Wahrscheinlichkeiten, sondern nur auf den relativen Häufigkeiten. Erst für $N → ∞$ stimmt diese Näherung mit $H(X)$ überein.
Beispiel 1: Wir kommen auf unser Würfel–Experiment zurück. Die folgende Tabelle zeigt die Wahrscheinlichkeitsfunktionen $P_R(R)$ und $P_B(B)$ für den roten und den blauen Würfel sowie die Näherungen $Q_R(R)$ und $Q_B(B)$, jeweils basierend auf dem Zufallsexperiment mit $N = 18$ Würfen. Die relativen Häufigkeiten $Q_R(R)$ und $Q_B(B)$ ergeben sich aus den beispielhaften Zufallsfolgen vom Beginn dieses Kapitels.
Für die Zufallsgröße $R$ gilt mit dem Logarithmus dualis (zur Basis 2):
$$H(R) = H(R) \big <div style="clear:both;"> </div> </div> =='"`UNIQ--h-4--QINU`"'Relative Entropie – Kullback–Leibler–Distanz == Wir betrachten die beiden Wahrscheinlichkeitsfunktionen $P_X(·)$ und $P_Y(·)$ über dem gleichen Alphabet $X$ = { $x_1$, $x_2$, ... , $x_M$ }, und definieren nun die '''relative Entropie''' (englisch: ''Informational Divergence'') zwischen diesen: $$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{M}
P_X(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x_{\mu})}{P_Y(x_{\mu})} \hspace{0.05cm}.$$
Bei Verwendung des Logarithmus zur Basis 2 ist wieder die Pseudo–Einheit „bit” hinzuzufügen. Man bezeichnet D(PX || PY) auch als die '''Kullback–Leibler–Distanz''' (kurz KL–Distanz). Diese liefert ein Maß für die „Ähnlichkeit” zwischen den beiden Wahrscheinlichkeitsfunktionen $P_X(·)$ und $P_Y(·)$:
In ähnlicher Weise lässt sich auch eine zweite Variante der Kullback–Leibler–Distanz angeben:
$$D(P_Y \hspace{0.05cm} || \hspace{0.05cm}P_X) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_Y(X)}{P_X(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{M}
P_Y(x_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_Y(x_{\mu})}{P_X(x_{\mu})} \hspace{0.05cm}.$$
Gegenüber der ersten Variante ist jede Funktion $P_X(·)$ durch $P_Y(·)$ ersetzt und umgekehrt. Da sich im allgemeinen $D(P_X || P_Y)$ und $D(P_Y || P_X)$ unterscheiden, ist der Begriff „Distanz” eigentlich irreführend. Wir wollen es aber bei dieser Namensgebung belassen.
Wertet man die beiden obigen Gleichungen aus, so erkennt man folgende Eigenschaften:
*Liegt genau die gleiche Verteilung vor ⇒ $P_Y(·) ≡ P_X(·)$, so ist $D(P_X || P_Y)$ = 0. In allen anderen Fällen ist $D(P_X || P_Y)$ > 0. Gleiches gilt für die zweite Variante $D(P_Y || P_X)$.
*Gilt $P_X(x_μ)$ ≠ 0 und $P_Y(x_μ)$ = 0 (es genügt ein einziges und ein beliebiges $μ$), so ergibt sich für die Kullback–Leibler–Distanz $D(P_X || P_Y)$ ein unendlich großer Wert.
*In diesem Fall ist $D(P_Y || P_X)$ nicht notwendigerweise ebenfalls unendlich. Diese Aussage macht nochmals deutlich, dass im allgemeinen $D(P_X || P_Y)$ ungleich $D(P_Y || P_X)$ sein wird.
Auf der nächsten Seite werden diese beiden Definitionen an unserem Standardbeispiel ''Würfel–Experiment'' verdeutlicht. Gleichzeitig verweisen wir auf folgende Aufgaben:
[[Aufgaben:3.04_KLD_%26_Binominalverteilung|A3.4: Kullback–Leibler–Distanz zur Binomialverteilung]]
[[Aufgaben:3.04Z_Nochmals_KL–Distanz|Z3.4: Nochmals Kullback–Leibler–Distanz]]
[[Aufgaben:3.05_Partitionierungsungleichung|A3.5: Partitionierungsungleichung]]
<div class="example">
Für unser Würfel–Experiment haben wir folgende Wahrscheinlichkeitsfunktionen $P_R(·)$ und $P_B(·)$ sowie deren Näherungen $Q_R(·)$ und $Q_B(·)$ definiert. Die Zufallsgröße $R$ bezeichnet hierbei die Augenzahl des roten Würfels und $B$ die Augenzahl des blauen Würfels. Die Näherungen $Q_R(·)$ und $Q_B(·)$ ergeben sich aus dem früher beschriebenen Experiment mit lediglich $N$ = 18 Doppelwürfen.
[[File:P_ID2745__Inf_T_3_1_S3_neu.png|Wahrscheinlichkeitsfunktionen unseres Würfelexperiments]]
*Da die Wahrscheinlichkeitsfunktionen $P_R(·)$ und $P_B(·)$ identisch sind, erhält man für die oben definierten Kullback–Leibler–Distanzen $D(P_R || P_B)$ und $D(P_B || P_R)$ jeweils 0.
*Der Vergleich von $P_R(·)$, $Q_R(·)$ ergibt für die erste Variante der Kullback–Leibler–Distanz
$$\begin{align*}D(P_R \hspace{0.05cm}|| \hspace{0.05cm} Q_R) \hspace{-0.15cm} & = \hspace{-0.15cm}
{\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_R(\cdot)}{Q_R(\cdot)}\right ]
\hspace{0.1cm} = \sum_{\mu = 1}^{6}
P_R(r_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{P_R(r_{\mu})}{Q_R(r_{\mu})} \hspace{0.05cm} = \\
\hspace{-0.15cm} & = \hspace{-0.15cm}\frac{1}{6} \cdot \left [
2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{2/18} \hspace{0.1cm} +
2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{3/18} \hspace{0.1cm} +
2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{1/6}{4/18} \hspace{0.1cm}
\right ] =\\
\hspace{-0.15cm} & = \hspace{-0.15cm} 1/6 \cdot \big [
2 \cdot 0.585 + 2 \cdot 0 - 2 \cdot 0.415 \big ] \approx 0.0570\,{\rm bit} \hspace{0.05cm}.\end{align*}$$
Hierbei wurde bei der vorzunehmenden Erwartungswertbildung die Tatsache ausgenutzt, dass wegen $P_R(r_1)$ = ... = $P_R(r_6)$ der Faktor 1/6 ausgeklammert werden kann. Da hier der Logarithmus zur Basis 2 verwendet wurde, ist die Pseudo–Einheit „bit” angefügt.
*Für die zweite Variante der Kullback–Leibler–Distanz ergibt sich ein etwas anderer Wert:
$$\begin{align*}D(Q_R \hspace{0.05cm}|| \hspace{0.05cm} P_R) \hspace{-0.15cm} & = \hspace{-0.15cm}
{\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{Q_R(\cdot)}{P_R(\cdot)}\right ]
\hspace{0.1cm} = \sum_{\mu = 1}^{6}
Q_R(r_{\mu}) \cdot {\rm log} \hspace{0.1cm} \frac{Q_R(r_{\mu})}{P_R(r_{\mu})} \hspace{0.05cm} = \\
\hspace{-0.15cm} & = \hspace{-0.15cm}2 \cdot \frac{2}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2/18}{1/6} \hspace{0.1cm} +
2 \cdot \frac{3}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{3/18}{1/6} \hspace{0.1cm} +
2 \cdot \frac{4}{18} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4/18}{1/6}
=\\
& = \hspace{-0.15cm}
4/18 \cdot (-0.585) + 3/18 \cdot 0 +8/18 \cdot 0.415 \approx 0.0544\,{\rm bit} \hspace{0.05cm}.\end{align*}$$
*Für den blauen Würfel erhält man $D(P_B || Q_B)$ ≈ 0.0283 bit und $D(Q_B || P_B)$ ≈ 0.0271 bit, also etwas kleinere KL–Distanzen, da sich die Approximation $Q_B(·)$ von $P_B(·)$ weniger unterscheidet als $Q_R(·)$ von $P_R(·)$.
*Vergleicht man die Häufigkeiten $Q_R(·)$ und $Q_B(·)$, so erhält man $D(Q_R || Q_B)$ ≈ 0.0597 bit und $D(Q_B || Q_R)$ ≈ 0.0608 bit. Hier sind die Distanzen am größten, da die Unterschiede zwischen $Q_B$ und $Q_R$ größer sind als zwischen $Q_R$ und $P_R $oder zwischen $Q_B$ und $P_B$.
<div style="clear:both;">
</div>
</div>
=='"`UNIQ--h-5--QINU`"'Verbundwahrscheinlichkeit und Verbundentropie ==
Für den Rest von Kapitel 3 betrachten wir stets zwei diskrete Zufallsgrößen $X$ = { $x_1$, $x_2$, ... , $x_M$ } und $Y$ = { $y_1$, $y_2$, ... , $y_K$ }, deren Wertebereiche nicht notwendigerweise übereinstimmen müssen. Das heißt: $K ≠ M$ (in anderer Notation: $|Y| ≠ |X|$) ist durchaus erlaubt.
Die Wahrscheinlichkeitsfunktion hat somit eine $K × M$–Matrixform mit den Elementen
$$P_{XY}(X = x_{\mu}\hspace{0.05cm}, Y = y_{\kappa}) = {\rm Pr} \big [( X = x_{\mu})\hspace{0.05cm}\cap \hspace{0.05cm} (Y = y_{\kappa}) \big ] \hspace{0.05cm}.$$
Als Kurzschreibweise verwenden wir $P_{XY}(X, Y)$, wobei $XY$ als neue Zufallsgröße zu interpretieren ist, die sowohl die Eigenschaften von $X$ als auch diejenigen von $Y$ beinhaltet.
<div class="definition">
Die '''Verbundentropie''' (englisch: ''Joint Entropy'') lässt sich als ein Erwartungswert mit der 2D–Wahrscheinlichkeitsfunktion $P_{XY}(X, Y)$ wie folgt darstellen:
$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] = \sum_{\mu = 1}^{M} \hspace{0.1cm} \sum_{\kappa = 1}^{K} \hspace{0.1cm}
P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa})} \hspace{0.05cm}.$$
<div style="clear:both;">
</div>
</div>
Im Folgenden verwenden wir durchgehend den Logarithmus zur Basis 2 ⇒ $\log(x) → \log_2(x)$ = $\text{ld}(x)$ ⇒ Logarithmus dualis. Der Zahlenwert ist somit mit der Pseudo–Einheit „bit” zu versehen.
Allgemein kann für die Verbundentropie die folgende '''obere Schranke''' angegegeben werden:
$$H(XY) \le H(X) + H(Y) \hspace{0.05cm}.$$
Diese Ungleichung drückt folgenden Sachverhalt aus:
*Das Gleichheitszeichen gilt nur für den Sonderfall statistisch unabhängiger Zufallsgrößen, wie im Beispiel C im nächsten Abschnitt anhand der Zufallsgrößen $R$ und $B$ demonstriert wird. Hierbei bezeichnen $R$ und $B$ die Augenzahlen eines roten und eines blauen Würfels.
*Gibt es dagegen statistische Abhängigkeiten wie im Beispiel D zwischen den Zufallsgrößen $R$ und $S$ = $R + B$, so gilt in obiger Gleichung das „<”–Zeichen: $H(RS) < H(R) + H(S)$.
In den Beispielen wird auch gezeigt, in wie weit sich die Verbundentropien $H(RB)$ und $H(RS)$ ändern, wenn man beim Würfel–Experiment nicht unendlich viele Wurfpaare ermittelt, sondern lediglich $N$ = 18.
<div class="example">
Wir kommen wieder auf das [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Einf.C3.BChrungsbeispiel_zur_statistischen_Abh.C3.A4ngigkeit_von_Zufallsgr.C3.B6.C3.9Fen|Würfel–Experiment]] zurück: Die Zufallsgrößen sind die Augenzahlen des roten und des blauen Würfels: $R$ = {1, 2, 3, 4, 5, 6}, $B$ = {1, 2, 3, 4, 5, 6}.
[[File:P_ID2747__Inf_T_3_1_S5a.png|2D–PMF <i>P<sub>RB</sub></i> und Näherung <i>Q<sub>RB</sub></i>]]
Die linke Grafik zeigt die Wahrscheinlichkeiten $P_{RB}(·)$, die sich für alle $μ$ = 1, ... , 6 und für alle $κ$ = 1, ... , 6 gleichermaßen zu 1/36 ergeben. Damit erhält man für die Verbundentropie:
$$H(RB) = H(RB) \big |_{N \hspace{0.05cm}\rightarrow \hspace{0.05cm}\infty} = {\rm log}_2 \hspace{0.1cm} (36) = 5.170\,{\rm bit} \hspace{0.05cm}.$$
Man erkennt aus obiger Grafik und der hier angegebenen Gleichung:
*Da $R$ und $B$ statistisch voneinander unabhängig sind, gilt $P_{RB}(R, B)$ = $P_R(R) · P_B(B)$.
*Die Verbundentropie ist die Summe der beiden Einzelentropien: $H(RB) = H(R) + H(B)$.
Die rechte Grafik zeigt die angenäherte 2D–Wahrscheinlichkeitsfunktion $Q_{RB}(·)$, basierend auf den nur $N$ = 18 Wurfpaaren unseres Experiments:
*Hier ergibt sich keine quadratische Form der Verbundwahrscheinlichkeit $Q_{RB}(·)$, und die daraus abgeleitete Verbundentropie ist deutlich kleiner als $H(RB)$:
$$H(RB) \big |_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 16 \cdot \frac{1}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{1} \hspace{0.1cm} +\hspace{0.1cm} 1 \cdot \frac{2}{18}\cdot {\rm log}_2 \hspace{0.1cm} \frac{18}{2} \hspace{0.1cm}= 4.059\,{\rm bit} \hspace{0.05cm}.$$
<div style="clear:both;">
</div>
</div>
<div class="example">
Bei unserem Würfel–Experiment haben wir neben den beiden Zufallsgrößen $R$ (roter Würfel) und $B$ (blauer Würfel) auch die Summe $S$ = $R + B$ betrachtet. Die linke Grafik zeigt, dass $P_{RS}(·)$ nicht als Produkt von $P_R(·)$ und $P_S(·)$ geschrieben werden kann. Mit den Wahrscheinlichkeitsfunktionen
$$\begin{align*}P_R(R) \hspace{-0.15cm} & = \hspace{-0.15cm} \left [ \hspace{0.1cm} 1/6\hspace{0.05cm}, 1/6\hspace{0.05cm}, 1/6\hspace{0.05cm}, 1/6\hspace{0.05cm}, 1/6\hspace{0.05cm}, 1/6 \hspace{0.1cm} \right ] \hspace{0.05cm},\\
P_S(S) \hspace{-0.15cm} & = \hspace{-0.15cm} \left [ \hspace{0.1cm} 1/36\hspace{0.05cm},2/36\hspace{0.05cm}, 3/36\hspace{0.05cm}, 4/36\hspace{0.05cm}, 5/36\hspace{0.05cm}, 6/36\hspace{0.05cm}, 5/36\hspace{0.05cm}, 4/36\hspace{0.05cm}, 3/36\hspace{0.05cm}, 2/36\hspace{0.05cm}, 1/36\hspace{0.1cm} \right ] \hspace{0.05cm} \end{align*}$$
erhält man für die Entropien:
$$\begin{align*}H(R) \hspace{-0.15cm} & = \hspace{-0.15cm} {\rm log}_2 \hspace{0.1cm} (6) \approx 2.585\,{\rm bit} \hspace{0.05cm},\\
H(S) \hspace{-0.15cm} & = & \hspace{-0.15cm} 2 \cdot \frac{1}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{1} \hspace{0.05cm} + 2 \cdot \frac{2}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{2} \hspace{0.05cm} + 2 \cdot \frac{3}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{3} \hspace{0.05cm} + 2 \cdot \frac{4}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{4} \hspace{0.05cm} +\\
& + \hspace{-0.15cm} 2 \cdot \frac{5}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{5}
+ 1 \cdot \frac{6}{36} \cdot {\rm log}_2 \hspace{0.05cm} \frac{36}{6} \approx 3.274\,{\rm bit} \hspace{0.05cm},
\\
H(RS) \hspace{-0.15cm} & = \hspace{-0.15cm} {\rm log}_2 \hspace{0.1cm} (36) \approx 5.170\,{\rm bit} \hspace{0.05cm}.\end{align*}$$
[[File:P_ID2748__Inf_T_3_1_S5b_neu.png|2D–PMF <i>P<sub>RS</sub></i> und Näherung <i>Q<sub>RS</sub></i>]]
Aus diesen Zahlenwerten erkennt man:
*Aufgrund der statistischen Abhängigkeit zwischen dem roten Würfel und der Summe ist die Verbundentropie $H(RS)$ ≈ 5.170 bit kleiner als $H(R)$ + $H(S)$ ≈ 5.877 bit.
*Der Vergleich mit Beispiel C zeigt, dass $H(RS)$ gleich $H(RB)$ ist. Der Grund ist, dass bei Kenntnis von $R$ die Zufallsgrößen $B$ und $S$ genau die gleichen Informationen liefern.
Rechts dargestellt ist der Fall, dass die 2D–PMF aus nur $N$ = 18 Wurfpaaren empirisch ermittelt wurde ⇒ $Q_{RS}(·)$. Obwohl sich aufgrund des sehr kleinen $N$–Wertes ein völlig anderes Bild ergibt, liefert die Näherung für $H(RS)$ den exakt gleichen Wert wie die Näherung für $H(RB)$:
$$H(RS) \big |_{N \hspace{0.05cm} = \hspace{0.05cm}18} = H(RB) \big |_{N \hspace{0.05cm} = \hspace{0.05cm}18} = 4.059\,{\rm bit} \hspace{0.05cm}.$$
Aufgaben zum Kapitel
Aufgabe 1.1Z: Binäre Entropiefunktion
Aufgabe 1.2: Entropie von Ternärquellen
Quellenverzeichnis
- ↑ Mecking, M.: Information Theory. Vorlesungsmanuskript, Lehrstuhl für Nachrichtentechnik, Technische Universität München, 2009.