Exercise 3.6: Partitioning Inequality

Die Kullback–Leibler–Distanz (kurz KLD) wird auch in der „Partitionierungsungleichung” (englisch: Partition Unequality) verwendet:

Wir gehen von der Menge $X = \{ x_1, \hspace{0.05cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.05cm} x_M \}$ und den Wahrscheinlichkeitsfunktionen

$$P_X(X) = P_X ( x_1, \hspace{0.05cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.05cm} x_M )\hspace{0.05cm},$$

$$Q_X(X) =Q_X ( x_1, \hspace{0.05cm} x_2, \text{...} \hspace{0.05cm}, \hspace{0.05cm} x_M ), $$

aus, die in irgendeiner Form „ähnlich” sein sollen.

Die Menge $X$ unterteilen wir in die Partitionen $A_1, \text{...} , A_K$ , die zueinander disjunkt sind und ein vollständiges System ergeben:

$X$$ = \big \{ \hspace{0.05cm} x_1, \hspace{0.05cm} x_2, ... \hspace{0.05cm}, \hspace{0.05cm} x_M \hspace{0.05cm} \big \}$$

Die Wahrscheinlichkeitsfunktionen bezüglich der Partitionierungen $A_1, A_2, \text{...} , A_K$ bezeichnen wir im Folgenden mit

$$P_X^{\hspace{0.15cm}(A)} = \left [ P_X ( A_1 )\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm},P_X ( A_K ) \right ],\hspace{0.05cm}\hspace{0.5cm}{\rm wobei}\hspace{0.15cm} P_X ( A_i ) = \sum_{ x \in A_i} P_X ( x )\hspace{0.05cm},$$

$$Q_X^{\hspace{0.15cm}(A)}= \left [ Q_X ( A_1 )\hspace{0.05cm}, \hspace{0.05cm}...\hspace{0.1cm},Q_X ( A_K ) \right ],\hspace{0.05cm}\hspace{0.40cm}{\rm wobei}\hspace{0.15cm} Q_X ( A_i ) = \sum_{ x \in A_i} Q_X ( x )\hspace{0.05cm}. $$

Die Partitionierungsungleichung liefert folgende Größenrelation hinsichtlich der Kullback–Leibler–Distanzen:

$$D(P_X^{\hspace{0.15cm}(A)} \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{\hspace{0.15cm}(A)}) \hspace{0.25cm}\le \hspace{0.25cm}D(P_X \hspace{0.05cm}\vert \vert \hspace{0.05cm} Q_X) \hspace{0.05cm}.$$

In Teilaufgabe (1) soll die Kullback–Leibler–Distanz der beiden Wahrscheinlichkeitsfunktionen $P_X(X)$ und $Q_X(X)$ für $X = \{0, 1, 2\}$ ⇒ $|X| = 3$ ermittelt werden. Anschließend soll die Menge $X$ mit $K = 2$ partitioniert werden entsprechend

$A = \{A_1 , A_2\}$ mit $A_1 =\{0\}$ und $A_2 = \{ 1,2 \}$ ,
$B = \{B_1 , B_2\}$ mit $B_1 =\{1\}$ und $B_2 = \{ 0,2 \}$,
$C = \{C_1 , C_2\}$ mit $C_1 =\{2\}$ und $C_2 = \{ 0,1\}$,

Anschließend sollen die jeweiligen Kullback–Leibler–Distanzen angegeben werden:

$D(P_X^{ (A) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (A) } )$,
$D(P_X^{ (B) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (B) } )$,
$D(P_X^{ (C) } \hspace{0.05cm} \vert \vert \hspace{0.05cm} Q_X^{ (C) } )$.

In der Teilaufgabe (5) wird schließlich nach den Bedingungen gefragt, damit in der obigen Ungleichung das Gleichheitszeichen zutrifft.

Hinweise:

Die Aufgabe gehört zum Kapitel Einige Vorbemerkungen zu den 2D-Zufallsgrößen.
Insbesondere wird Bezug genommen auf die Seite Relative Entropie – Kullback-Leibler-Distanz.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
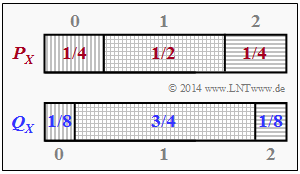
Die beiden Wahrscheinlichkeitsfunktionen können aus obiger Grafik wie folgt abgelesen werden:

$$P_X(X) = [1/4 , 1/2 , 1/4],$$

$$Q_X(X) = [1/8 , 3/4, 1/8].$$

Fragebogen

$ D(P_X \parallel Q_X)$ =

$bit$

$D(P_X^{ (A) } \parallel Q_X^{ (A) } )$ =

$bit$

$D(P_X^{ (B) } \parallel Q_X^{ (B) } )$ =

$bit$

	Das gleiche Ergebnis wie für die Partitionierung $A$.
	Das gleiche Ergebnis wie für die Partitionierung $B$.
	Ein ganz anderes Ergebnis.

	Es müssen $\|X\|$ Gleichungen erfüllt sein.
	Für $x \epsilon A_i$ muss gelten : $P_X(x)/Q_X(x) = P_X(A_i)/ Q_X(A_i)$

Musterlösung

Solution

1. Für die Kullback–Leibler–Distanz (KLD) gilt:

$$D(P_X \parallel P_Y) = E [ log_2 \frac{P_X(X)}{P_Y(X)}] = \sum\limits_{ x \epsilon X} P_X(x) . log_2 \frac{P_X(x)}{P_Y(x)} =$$

$$\frac{1}{2} . log_2 \frac{1/2}{3/4} + 2 . \frac{1}{4} . log_2 \frac{1/4}{1/8} +log_2 \frac{2}{3} + \frac{1}{2} . log_2(2) =$$

$$1 - \frac{1}{2} . log_2(3) = 0.2075 (bit)$$

2. $Partitionierung A \Rightarrow A_1 = \{0\}$ , $A_2 = \{ 1 , 2 \}$ : Man erhält die Wahrscheinlichkeitsfunktionen $P_X^{ (A) } (X) = \{1/4 , 3/4\}$ und $Q_X^{ (A) } (X) = \{1/8 , 7/8\}$. Daraus folgt:

$$D(P_X^{ (A) } \parallel Q_X^{ (A) } )$ = \frac{1}{4} . log_2 \frac{1/4}{1/8} + \frac{3}{4} . log_2 \frac{3/4}{7/8} =$$

$$ = \frac{1}{4} . log_2 (2) + \frac{3}{4} . log_2 \frac{6}{7} = 0.0832 (bit)$$ Es ergibt sich also eine kleinere KLD als in Teilaufgabe (a).

3. $Partitionierung B \Rightarrow B_1 = \{1\}$ , $B_2 = \{ 0 , 2 \}$ : Man erhält die Wahrscheinlichkeitsfunktionen $P_X^{ (B) } (X) = \{1/2 , 1/2\}$ und $Q_X^{ (B) } (X) = \{3/4 , 1/4\}$. Analog zur Teilaufgabe (b) erhält man nun:

$$D(P_X^{ (B) } \parallel Q_X^{ (B) } ) = \frac{1}{2} . log_2 \frac{1/2}{3/4} + \frac{1}{2} . log_2 \frac{1/2}{1/4} = 0.2075$$ $\Rightarrow$ gleiches Ergebnis wie in Aufgabe (a) $\Rightarrow$ Bei Partitionierung (B) gilt das Gleichheitszeichen.

4.$Partitionierung C \Rightarrow C_1 = \{2\}$ , $C_2 = \{ 0 , 1\}$ : Man erhält $P_X^{ (C) } (X) = \{1/4, 3/4\}$ , $Q_X^{ (C) } (X) = \{1/8, 7/8\}$ . also die gleichen Funktionen wie bei der Partitionierung $A \Rightarrow Lösungsvorschlag 1$.

5. Partitionierung $B$ hat zum Ergebnis $D(P_X^{ (B) } \parallel Q_X^{ (B) } ) = D(P_X \parallel Q_X)$ geführt. Für diesen Fall ist

$\frac{P_X(1)}{Q_X(1)} = \frac{1/2}{3/4} = \frac{2}{3}$ , $\frac{P_X(B_1)}{Q_X(B_1)} = \frac{1/2}{3/4} = \frac{2}{3}$,

$\frac{P_X(0)}{Q_X(0)} = \frac{1/4}{1/8} = 2$ , $\frac{P_X(B_2)}{Q_X(B_2)} = \frac{1/2}{1/4} = 2$,

$\frac{P_X(2)}{Q_X(2)} = \frac{1/4}{1/8} = 2$ , $\frac{P_X(B_2)}{Q_X(B_2)} = \frac{1/2}{1/4} = 2$

Es muss also für alle $x \epsilon X$ gelten :

$\frac{P_X(x)}{Q_X(x)} = \frac{P_X(B_1)}{Q_X(B_1)} $ , falls $ x \epsilon B_1$

$\frac{P_X(x)}{Q_X(x)} = \frac{P_X(B_2)}{Q_X(B_2)} $ , falls $ x \epsilon B_2$

Durch Verallgemeinerung erhält man, dass $beide Lösungsvorschläge$ richtig sind.