Im letzten Kapitel dieses Buches werden die bisher für den wertdiskreten Fall definierten informationstheoretischen Größen derart adaptiert, dass sie auch für wertkontinuierliche Zufallsgrößen angewandt werden können. Aus der Entropie $H(X)$ für die wertdiskrete Zufallsgröße $X$ wird so zum Beispiel im wertkontinuierlichen Fall die differentielle Entropie $h(X)$. Während $H(X)$ die „Unsicherheit” hinsichtlich der diskreten Zufallsgröße $X$ angibt, kann $h(X)$ einer kontinuierlichen Zufallsgröße nicht in gleicher Weise interpretiert werden.
Viele der im dritten Kapitel „Information zwischen zwei wertdiskreten Zufallsgrößen ⇒ siehe Inhaltsverzeichnis für die herkömmliche Entropie hergeleiteten Zusammenhänge gelten auch für die differentielle Entropie. So kann auch für wertkontinuierliche Zufallsgrößen $X$ und $Y$ die differentielle Verbundentropie $h(XY)$ angegeben werden und ebenso die beiden bedingten differentiellen Entropien $h(Y|X)$ und $h(X|Y)$.
Contents
- 1 Eigenschaften wertkontinuierlicher Zufallsgrößen
- 2 Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung
- 3 Definition und Eigenschaften der differentiellen Entropie
- 4 Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen
- 5 Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen
- 6 WDF–Herleitung für maximale differentielle Entropie
- 7 Aufgaben zu Kapitel 4.1
Eigenschaften wertkontinuierlicher Zufallsgrößen
Bisher wurden stets wertdiskrete Zufallsgrößen der Form $X = \{x_1, x_2, \text{...} , x_μ, \text{...} , x_M\}$ betrachtet, die aus informationstheoretischer Sicht vollständig durch ihre Wahrscheinlichkeitsfunktion (englisch: Probability Mass Function, PMF) $P_X(X)$ charakterisiert werden:
- $$P_X(X) = \left [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_{\mu},\hspace{0.05cm} \text{...}\hspace{0.15cm}, p_M \hspace{0.1cm}\right ] \hspace{0.3cm}{\rm mit} \hspace{0.3cm} p_{\mu}= P_X(x_{\mu})= {\rm Pr}( X = x_{\mu}) \hspace{0.05cm}.$$
Eine wertkontinuierliche Zufallsgröße kann dagegen – zumindest in endlichen Intervallen – jeden beliebigen Wert annehmen. Aufgrund des nicht abzählbaren Wertevorrats ist in diesem Fall die Beschreibung durch eine Wahrscheinlichkeitsfunktion nicht möglich oder zumindest nicht sinnvoll: Es ergäbe sich nämlich $M \to ∞$ sowie $p_1 \to 0$, $p_2 \to 0$, usw.
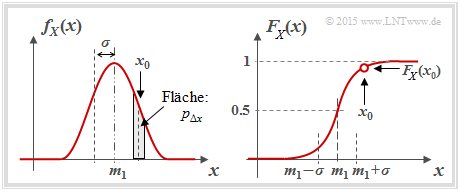
Man verwendet zur Beschreibung wertkontinuierlicher Zufallsgrößen gemäß den Definitionen im Buch Stochastische Signaltheorie gleichermaßen (beachten Sie die Einträge in der Grafik):
- die Wahrscheinlichkeitsdichtefunktion (WDF, englisch: Probability Density Function, PDF):
- $$f_X(x_0)= \lim_{{\rm \Delta} x\to \rm 0}\frac{p_{{\rm \Delta} x}}{{\rm \Delta} x} = \lim_{{\rm \Delta} x\to \rm 0}\frac{{\rm Pr} \{ x_0- {\rm \Delta} x/\rm 2 \le \it X \le x_{\rm 0} +{\rm \Delta} x/\rm 2\}}{{\rm \Delta} x};$$
- In Worten: Der WDF–Wert bei $x_0$ gibt die Wahrscheinlichkeit $p_{Δx}$ an, dass die Zufallsgröße $X$ in einem (unendlich kleinen) Intervall der Breite $Δx$ um $x_0$ liegt, dividiert durch $Δx$;
- den Mittelwert (Moment erster Ordnung, englisch: Mean Value bzw. Expectation Value):
- $$m_1 = {\rm E}[ X]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} x \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$
- die Varianz (Zentralmoment zweiter Ordnung, englisch: Variance):
- $$\sigma^2 = {\rm E}[(X- m_1 )^2]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} (x- m_1 )^2 \cdot f_X(x- m_1 ) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$
- die Verteilungsfunktion (VTF, englisch: Cumulative Distribution Function, CDF):
- $$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$
Beachten Sie, dass sowohl die WDF–Fläche als auch der VTF–Endwert stets gleich 1 sind.
Nomenklaturhinweise zu WDF und VTF Wir verwenden in diesem Kapitel für eine Wahrscheinlichkeitsdichtefunktion die in der Literatur häufig verwendete Darstellungsform $f_X(x)$, wobei gilt:
- $X$ bezeichnet die (wertdiskrete oder wertkontinuierliche) Zufallsgröße,
- $x$ ist eine mögliche Realisierung von $X$ ⇒ $x ∈ X$.
Entsprechend bezeichnen wir die Verteilungsfunktion (VTF) der Zufallsgröße $X$ mit $F_X(x)$ entsprechend folgender Definition:
- $$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$
In anderen LNTwww–Büchern schreiben wir oft, um nicht für eine Variable zwei Zeichen zu verbrauchen:
- für die WDF $f_x(x)$ ⇒ keine Unterscheidung zwischen Zufallsgröße und Realisiering,
- für die VTF $F_x(r) = {\rm Pr}(x ≤ r)$ ⇒ hier benötigt man auf jeden Fall eine zweite Variable.
Wir bitten, diese formale Ungenauigkeit zu entschuldigen.
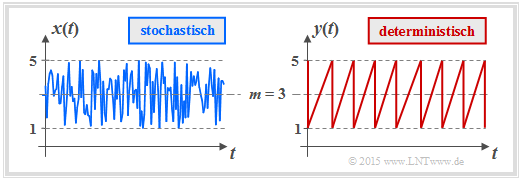
Beispiel 1: Wir betrachten nun mit der Gleichverteilung einen wichtigen Sonderfall. Die Grafik zeigt den Verlauf zweier gleichverteilter Größen, die alle Werte zwischen 1 und 5 (Mittelwert $m_1$ = 3) mit gleicher Wahrscheinlichkeit annehmen können. Links ist das Ergebnis eines Zufallsprozesses dargestellt, rechts ein deterministisches Signal („Sägezahn”) mit gleicher Amplitudenverteilung.
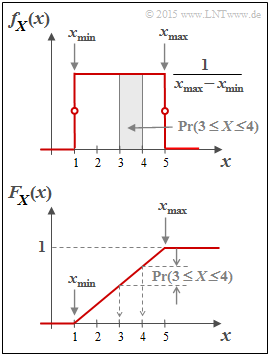
- $$f_X(x) = \left\{ \begin{array}{c} \hspace{0.25cm}(x_{\rm max} - x_{\rm min})^{-1} \\ (x_{\rm max} - x_{\rm min})^{-1}/2 \\ \hspace{0.25cm} 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ \end{array} \begin{array}{*{20}l} {x_{\rm min} < x < x_{\rm max},} \\ x ={x_{\rm min} \hspace{0.1cm}{\rm und}\hspace{0.1cm}x = x_{\rm max},} \\ x > x_{\rm max}. \\ \end{array}$$
Es ergeben sich hier für den Mittelwert $m_1$ = ${\rm E}[X]$ und die Varianz $σ_2$ = ${\rm E}[(X – m_1)^2]$ folgende Gleichungen:
- $$m_1 = \frac{x_{\rm max} + x_{\rm min} }{2}\hspace{0.05cm}, \hspace{0.5cm} \sigma^2 = \frac{(x_{\rm max} - x_{\rm min})^2}{12}\hspace{0.05cm}.$$
Unten dargestellt ist die Verteilungsfunktion (VTF):
- $$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$
Diese ist für $x ≤ x_{\rm min}$ identisch $0$, steigt danach linear an und erreicht bei $x = x_{\rm max}$ den VTF–Endwert $1$. Die Wahrscheinlichkeit, dass die Zufallgröße $X$ einen Wert zwischen $3$ und $4$ annimmt, kann sowohl aus der WDF als auch aus der VTF ermittelt werden:
- $${\rm Pr}(3 \le X \le 4) = \int_{3}^{4} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi = 0.25\hspace{0.05cm}\hspace{0.05cm},$$
- $${\rm Pr}(3 \le X \le 4) = F_X(4) - F_X(3) = 0.25\hspace{0.05cm}.$$
Weiterhin ist zu beachten:
- Das Ergebnis $X = 0$ ist bei dieser Zufallsgröße ausgeschlossen ⇒ ${\rm Pr}(X = 0) = 0$.
- Das Ergebnis $X = 4$ ist dagegen durchaus möglich. Trotzdem gilt auch hier ${\rm Pr}(X = 4) = 0$.
Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung
Wir betrachten nun eine wertkontinuierliche Zufallsgröße $X$ im Bereich von $0$ bis $1$.
- Wir quantisieren die kontinuierliche Zufallsgröße $X$, um die bisherige Entropieberechnung weiter anwenden zu können. Die so entstehende diskrete (quantisierte) Größe nennen wir $Z$.
- Die Quantisierungsstufenzahl sei $M$, so dass jedes Quantisierungsintervall $μ$ bei der vorliegenden WDF die Breite ${\it Δ} = 1/M$ aufweist. Die Intervallmitten bezeichnen wir mit $x_μ$.
- Die Wahrscheinlichkeit $p_μ = {\rm Pr}(Z = z_μ)$ bezüglich $Z$ ist gleich der Wahrscheinlichkeit, dass die kontinuierliche Zufallsgröße $X$ einen Wert zwischen $x_μ – {\it Δ}/2$ und $x_μ + {\it Δ}/2$ besitzt.
- Zunächst setzen wir $M = 2$ und verdoppeln anschließend $M$ in jeder Iteration. Dadurch wird die Quantisierung zunehmend feiner. Im $n$–ten Versuch gilt dann $M = 2^n$ und ${\it Δ} =2^{–n}$.
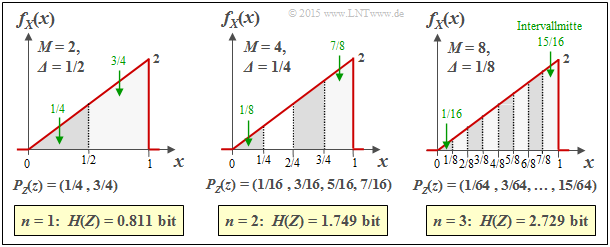
Beispiel 2: Die Grafik zeigt die Ergebnisse der ersten drei Versuche für eine dreieckförmige WDF (zwischen 0 und 1):
- $n = 1 \ ⇒ \ M = 2 \ ⇒ \ {\it Δ} = 1/2\text{:} \ H(Z) = 0.811\ \rm bit$,
- $n = 2 \ ⇒ \ M = 4 \ ⇒ \ {\it Δ} = 1/4\text{:} \ H(Z) = 1.749\ \rm bit$,
- $n = 3 \ ⇒ \ M = 8 \ ⇒ \ {\it Δ} = 1/8\text{:} \ H(Z) = 2.729\ \rm bit$.
Entropiebestimmung der Dreieck–WDF nach Quantisierung
Zudem können der Grafik noch folgende Größen entnommen werden, zum Beispiel für ${\it Δ} = 1/8$:
- Die Intervallmitten liegen bei $x_1 = 1/16, x_2 = 3/16,\text{ ...} \ , x_8 = 15/16 \ ⇒ \ x_μ = {\it Δ} · (μ – 1/2)$.
- Die Intervallflächen ergeben sich zu $p_μ = {\it Δ} · f_X(x_μ) \ ⇒ \ p_8 = 1/8 · (7/8+1)/2 = 15/64$.
- Damit erhält man $P_Z(Z) = (1/64, 3/64, 5/64, 7/64, 9/64, 11/64, 13/64, 15/64)$.
Die Ergebnisse dieses Experiments interpretieren wir wie folgt:
- Die Entropie $H(Z)$ nimmt mit steigendem $M$ immer mehr zu.
- Der Grenzwert von $H(Z)$ für $M \to ∞ \ ⇒ \ {\it Δ} → 0$ ist unendlich.
- Damit ist auch die Entropie $H(X)$ der wertkontinuierlichen Zufallsgröße $X$ unendlich groß.
- Daraus folgt: Die bisherige Entropie–Definition versagt hier.
Zur Verifizierung unseres empirischen Ergebnisses gehen wir von folgender Gleichung aus:
- $$H(Z) = \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} p_{\mu} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\mu}}= \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} {\it \Delta} \cdot f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{{\it \Delta} \cdot f_X(x_{\mu} )}\hspace{0.05cm}.$$
- Wir spalten nun $H(Z) = S_1 + S_2$ in zwei Summen auf:
- $$\begin{align*}S_1 & = {\rm log}_2 \hspace{0.1cm} \frac{1}{\it \Delta} \cdot \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.02cm} {\it \Delta} \cdot f_X(x_{\mu} ) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.05cm},\\ S_2 & = \hspace{0.05cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x_{\mu} ) } \cdot {\it \Delta} \hspace{0.2cm}\approx \hspace{0.2cm} \int_{0}^{1} \hspace{0.05cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$
Die Näherung $S_1 ≈ –\log_2 {\it Δ}$ gilt exakt nur im Grenzfall ${\it Δ} → 0$. Die angegebene Näherung für $S_2$ gilt ebenfalls nur für kleine ${\it Δ} → {\rm d}x$, so dass man die Summe durch das Integral ersetzen kann.
Verallgemeinerung: Nähert man die wertkontinuierliche Zufallsgröße $X$ mit der WDF $f_X(x)$ durch eine wertdiskrete Zufallsgröße $Z$ an, indem man eine (feine) Quantisierung mit der Intervallbreite ${\it Δ}$ durchführt, so erhält man für die Entropie der Zufallsgröße $Z$:
- $$H(Z) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm}+ \hspace{-0.35cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x = - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm} + h(X) \hspace{0.5cm}[{\rm in \hspace{0.15cm}bit}] \hspace{0.05cm}.$$
Das Integral beschreibt die differentielle Entropie $h(X)$ der wertkontinuierlichen Zufallsgröße $X$. Für den Sonderfall ${\it Δ} = 1/M = 2^{–n}$ kann die obige Gleichung auch wie folgt geschrieben werden:
- $$H(Z) = n + h(X) \hspace{0.5cm}[{\rm in \hspace{0.15cm}bit}] \hspace{0.05cm}.$$
- Im Grenzfall ${\it Δ} → 0 ⇒ M → ∞ ⇒ n → ∞$ ist auch die Entropie der wertkontinuierlichen Zufallsgröße unendlich groß: $H(X) → ∞$.
- Auch bei kleinerem $n$ stellt diese Gleichung lediglich eine Näherung für $H(Z)$ dar, wobei die differentielle Entropie $h(X)$ der wertkontinuierlichen Größe als Korrekturfaktor dient.
Beispiel 3: Wir betrachten wie im Beispiel 2 eine Dreieck–WDF (zwischen $0$ und $1$). Deren differentielle Entropie ergibt sich, wie in der Aufgabe 4.2 berechnet, zu $h(X) = \hspace{0.05cm}–0.279 \ \rm bit$ .
- In der Tabelle ist die Entropie $H(Z)$ der mit $n$ Bit quantisierten Größe $Z$ angegeben.
- Man erkennt bereits für $n = 3$ eine gute Übereinstimmung zwischen der Näherung (untere Zeile) und der exakten Berechnung (Zeile 2).
Definition und Eigenschaften der differentiellen Entropie
Die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße $X$ lautet mit der Wahrscheinlichkeitsdichtefunktion $f_X(x)$:
$$h(X) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{{\rm supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} [ f_X(x) ] \hspace{0.1cm}{\rm d}x \hspace{0.6cm}{\rm mit}\hspace{0.6cm} {\rm supp}(f_X) = \{ x: f_X(x) > 0 \} \hspace{0.05cm}.$$
Hinzugefügt werden muss jeweils eine Pseudo–Einheit:
- „nat” bei Verwendung von „ln” ⇒ natürlicher Logarithmus,
- „bit” bei Verwendung von „log2” ⇒ Logarithmus dualis.
Während für die (herkömmliche) Entropie einer wertdiskreten Zufallsgröße $X$ stets $H(X) ≥ 0$ gilt, kann die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße auch negativ sein. Daraus ist bereits ersichtlich, dass $h(X)$ im Gegensatz zu $H(X)$ nicht als „Unsicherheit” interpretiert werden kann.
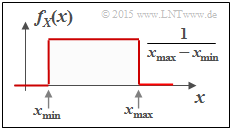Die Grafik zeigt die Wahrscheinlichkeitsdichte einer zwischen $x_{\rm min}$ und $x_{\rm max}$ gleichverteilten Zufallsgröße $X$. Für deren differentielle Entropie erhält man in „nat”:
$$\begin{align*}h(X) \hspace{-0.18cm} & = \hspace{-0.18cm} - \hspace{-0.18cm}\int\limits_{x_{\rm min}}^{x_{\rm max}} \hspace{-0.28cm} \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min}} \cdot {\rm ln} \hspace{0.1cm} [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min}} ] \hspace{0.1cm}{\rm d}x & = \hspace{-0.18cm} {\rm ln} \hspace{0.1cm} [ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min}} ] \cdot [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min}} ]_{x_{\rm min}}^{x_{\rm max}}={\rm ln} \hspace{0.1cm} [ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min}} ]\hspace{0.05cm}.\end{align*} $$
Die Gleichung für die differentielle Entropie in „bit” lautet: $h(X) = \log_2 [x_{\rm max} – x_{ \rm min}]$.
Die Grafik zeigt anhand einiger Beispiele die numerische Auswertung des obigen Ergebnisses. Auf der nächsten Seite wird auf die Größen $h_1(X), ... , h_6(X)$ näher eingegangen.
Aus den Skizzen des letzten Beispiels lassen sich wichtige Eigenschaften der differentiellen Entropie $h(X)$ ablesen:
- Die differentielle Entropie wird durch eine WDF–Verschiebung (um $k$) nicht verändert:
$$h(X + k) = h(X) \hspace{1.7cm}\Rightarrow \hspace{0.2cm} h_3(X) = h_4(X) = h_5(X) \hspace{0.05cm}.$$
- $h(X)$ ändert sich durch Stauchung/Spreizung der WDF um den Faktor $k ≠ 0$ wie folgt:
$$h( k\hspace{-0.05cm} \cdot \hspace{-0.05cm}X) = h(X) + {\rm log}_2 \hspace{0.05cm} |k|\hspace{0.15cm}\Rightarrow \hspace{0.15cm} h_6(X) = h_5(AX) = h_5(X) + {\rm log}_2 \hspace{0.05cm} (A) = {\rm log}_2 \hspace{0.05cm} (2A) \hspace{0.05cm}.$$
Des Weiteren gelten viele der in Kapitel 3 für den wertdiskreten Fall hergeleitete Gleichungen auch für wertkontinuierliche Zufallsgrößen. Aus der folgenden Zusammenstellung erkennt man, dass oft nur das „$H$” durch ein „$h$” sowie die PMF durch die entsprechende WDF zu ersetzen ist.
- Bedingte differentielle Entropie (englisch: Conditional Differential Entropy):
$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{-0.4cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.05cm}$$
$$\Rightarrow \hspace{0.3cm}h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
- Differentielle Verbundentropie (englisch: Joint Differential Entropy):
$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.4cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ P_{XY}(x, y)} \hspace{0.05cm}$$
$$\Rightarrow \hspace{0.3cm}h(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{f_{XY}(X, Y)}\right ] =\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_{XY}(x, y) } \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
- Kettenregel der differentiellen Entropie:
$$H(X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} H(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} H(X_i) \hspace{0.05cm}$$
$$\Rightarrow \hspace{0.3cm} h(X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} h(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}... \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} h(X_i) \hspace{0.05cm}.$$
- Kullback–Leibler–Distanz zwischen den Zufallsgrößen $X$ und $Y$:
$$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{X})\hspace{-0.8cm}} P_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x)}{P_Y(x)} \ge 0$$
$$\Rightarrow \hspace{0.3cm}D(f_X \hspace{0.05cm} || \hspace{0.05cm}f_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{f_X(X)}{f_Y(X)}\right ] \hspace{0.2cm}= \hspace{-0.4cm}\int\limits_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{f_X(x)}{f_Y(x)} \hspace{0.15cm}{\rm d}x \ge 0 \hspace{0.05cm}.$$
Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen
Die Tabelle zeigt die Ergebnisse für drei beispielhafte Wahrscheinlichkeitsdichtefunktionen $f_X(x)$. Diese sind alle spitzenwertbegrenzt, das heißt, es gilt jeweils $|X| ≤ A$.
[[File: P_ID2867__Inf_A_4_1.png|Differentielle Entropie spitzenwertbegrenzter Zufallsgrößen]]
Bei Spitzenwertbegrenzung kann man die differentielle Entropie stets wie folgt darstellen:
$$h(X) = {\rm log}\,\, ({\it \Gamma}_{\rm A} \cdot A).$$
Das Argument $Γ_A · A$ ist unabhängig davon, welchen Logarithmus man verwendet. Anzufügen ist
- bei Verwendung von „ln” ist die Pseudo–Einheit „nat”,
- bei Verwendung von „log2” ist die Pseudo–Einheit „bit”.
Theorem: Unter der Nebenbedingung Spitzenwertbegrenzung (englisch: Peak Constraint) ⇒ also WDF $f_X(x) = 0$ für $|x| > A$ – führt die Gleichverteilung zur maximalen differentiellen Entropie:
$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} (2A)\hspace{0.05cm}.$$
Das Theorem bedeutet gleichzeitig, dass bei jeder anderen spitzenwertbegrenzten WDF (außer der Gleichverteilung) der Kennparameter $Γ_A$ kleiner als 2 sein wird.
- Für die symmetrische Dreieckverteilung ergibt sich nach obiger Tabelle $Γ_A = e^{1/2} ≈ 1.649$.
- Beim einseitigen Dreieck (zwischen 0 und $A$) ist demgegenüber $Γ_A$ nur halb so groß.
- Auch für jedes andere Dreieck (Breite $A$, Spitze beliebig zwischen 0 und $A$) gilt $Γ_A ≈ 0.824$.
Die jeweils zweite $h(X)$–Angabe und die Kenngröße $Γ_L$ eignet sich dagegen für den Vergleich von Zufallsgrößen bei Leistungsbegrenzung – siehe nächste Seite. Unter dieser Nebenbedingung ist die symmetrische Dreieckverteilung $(Γ_L ≈ 16.31)$ besser als die Gleichverteilung $(Γ_L = 12)$.
Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen
Die differentielle Entropie $h(X)$ für drei beispielhafte Dichtefunktionen $f_X(x)$, die alle die gleiche Varianz $σ_2 = {\rm E}[|X –m_x|^2]$ ⇒ Streuung $σ$ aufweisen, sind der folgenden Tabelle zu entnehmen:
- Gaußverteilung ⇒ siehe Buch Stochastische Signaltheorie, Kapitel 3.5,
- Laplaceverteilung ⇒ siehe Buch Stochastische Signaltheorie, Kapitel 3.6,
- Exponentialverteilung ⇒ siehe Buch Stochastische Signaltheorie, Kapitel 3.6.
Die differentielle Entropie lässt sich bei allen diesen Beispielen als
$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm L} \cdot \sigma^2)$$
darstellen. Das Ergebnis unterscheidet sich nur durch die Pseudo–Einheit „nat” bei Verwendung von „ln” bzw. „bit” bei Verwendung von „log2”.
Theorem: Unter der Nebenbedingung der Leistungsbegrenzung (englisch: Power Constraint) führt die Gaußverteilung
$$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2}} \cdot {\rm exp} \left [ - \hspace{0.05cm}\frac{(x - m_1)^2}{2 \sigma^2}\right ]$$
unabhängig vom Mittelwert $m_1$ zur maximalen differentiellen Entropie:
$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$
Beweis
Dies bedeutet gleichzeitig, dass für jede andere WDF als die Gaußverteilung $Γ_L < 2πe ≈ 17.08$ gelten muss. Beispielsweise ergibt sich der Kennwert $Γ_L = 6e ≈ 16.31$ für die Dreieckverteilung, $Γ_L = 2e^2 ≈ 14.78$ für die Laplaceverteilung und $Γ_L = 12$ für die Gleichverteilung.
WDF–Herleitung für maximale differentielle Entropie
Beweis für Spitzenwertbegrenzung ⇒ $\mathbf{|X| ≤ A}$: Unter der Nebenbedingung des Spitzenwertbegrenzung gilt für die differentielle Entropie:
$$h(X) = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Von allen möglichen Wahrscheinlichkeitsdichtefunktionen $f_X(x)$, die die Bedingung
$$\int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x = 1$$
erfüllen, ist nun diejenige Funktion $g_X(x)$ gesucht, die zur maximalen differentiellen Entropie $h(X)$ führt. Zur Herleitung benutzen wir das Verfahren der [[1]]:
- Wir definieren die Lagrange–Kenngröße $L$ in der Weise, dass darin sowohl $h(X)$ als auch die Nebenbedingung $|X| ≤ A$ enthalten sind:
$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.5cm}+ \hspace{0.5cm} \lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
- Wir setzen allgemein $f_X(x) = g_X(x) + ε · ε_X(x)$, wobei $ε_X(x)$ eine beliebige Funktion darstellt, mit der Einschränkung, dass die WDF–Fläche gleich 1 sein muss. Damit erhalten wir:
$$\begin{align*}L \hspace{-0.15cm} & = \hspace{-0.15cm} \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) ] \cdot {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) + \varepsilon \cdot \varepsilon_X(x) } \hspace{0.1cm}{\rm d}x + \\ & + \hspace{-0.15cm}\lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) ] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$
- Die bestmögliche Funktion ergibt sich dann, wenn es für $ε = 0$ eine stationäre Lösung gibt:
$$\left [\frac{{\rm d}L}{{\rm d}\varepsilon} \right ]_{\varepsilon \hspace{0.05cm}= \hspace{0.05cm}0}=\hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \cdot \left [ {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 \right ]\hspace{0.1cm}{\rm d}x \hspace{0.3cm} + \hspace{0.3cm}\lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \hspace{0.1cm}{\rm d}x \stackrel{!}{=} 0 \hspace{0.05cm}.$$
- Diese Bedingungsgleichung ist unabhängig von $ε_X$ nur dann zu erfüllen, wenn gilt:
$${\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 + \lambda = 0 \hspace{0.4cm} \forall x \in [-A, +A]\hspace{0.3cm} \Rightarrow\hspace{0.3cm} g_X(x) = {\rm const.}\hspace{0.4cm} \forall x \in [-A, +A]\hspace{0.05cm}.$$
Resümee: Die maximale differentielle Entropie ergibt sich unter der Nebenbedingung $\mathbf{|X| ≤ A}$ für die gleichverteilte Zufallsgröße (englisch: Uniform PDF):
$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm A} \cdot A) = {\rm log} \hspace{0.1cm} (2A) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm A} = 2 \hspace{0.05cm}.$$
Jede andere Zufallsgröße mit der WDF–Eigenschaft $f_X(|x| > A)$ = 0 führt zu einer kleineren differentiellen Entropie, gekennzeichnet durch den Parameter $Γ_A$ < 2.
Beweis für Leistungsbegrenzung ⇒ $\mathbf{{\rm E}[|X – m_1|^2] ≤ σ^2}$:
Vorneweg zur Begriffserklärung: Eigentlich wird nicht die Leistung ⇒ das zweite Moment $m_2$ begrenzt, sondern das zweite Zentralmoment ⇒ Varianz $μ_2 = σ^2$. Lassen wir nur mittelwertfreie Zufallsgrößen zu, so umgehen wir das Problem. Damit lautet die Laplace–Kenngröße:
$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_1 \cdot \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_2 \cdot \int_{-\infty}^{+\infty}\hspace{-0.1cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Nach ähnlichem Vorgehen wie im Fall der Spitzenwertbegrenzung erhält man das Ergebnis, dass die „bestmögliche” WDF $g_X(x)$ proportinonal zu ${\rm exp}(–λ_2 · x^2)$ sein muss ⇒ Gaußverteilung:
$$g_X(x) ={1}/{\sqrt{2\pi \sigma^2}} \cdot {\rm exp} \left ( - \hspace{0.05cm}{x^2}/{(2 \sigma^2)}\right )\hspace{0.05cm}.$$
Wir verwenden hier aber für den expliziten Beweis zur Abwechslung die Kullback–Leibler–Distanz zwischen einer geeigneten allgemeinen WDF $f_X(x)$ und der Gauß–WDF $g_X(x)$:
$$D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \frac{f_X(x)}{g_X(x)} \hspace{0.1cm}{\rm d}x = -h(X) - I_2$$
$$\Rightarrow\hspace{0.3cm}I_2 = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} {g_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Zur Vereinfachung wurde hier der natürliche Logarithmus verwendet. Damit erhalten wir:
$$I_2 = - \frac{1}{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{-0.4cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.3cm}- \hspace{0.3cm} \frac{1}{2\sigma^2} \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{0.02cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$
Das erste Integral ist definitionsgemäß gleich 1 und das zweite Integral ergibt $σ^2$:
$$I_2 = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) - {1}/{2} \cdot [{\rm ln} \hspace{0.1cm} ({\rm e})] = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)$$
$$\Rightarrow\hspace{0.3cm} D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = -h(X) - I_2 = -h(X) + {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$
Da auch bei wertkontinuierlichen Zufallsgrößen die Kullback–Leibler–Distanz größer oder gleich 0 ist, erhält man nach Verallgemeinerung (ln ⇒ log):
$$h(X) \le {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$
Das Gleichzeichen gilt nur, wenn die Zufallsgröße $X$ gaußverteilt ist.
Resümee: Die maximale differentielle Entropie unter der Nebenbedingung $\mathbf{|X – m_1|^2 ≤ σ^2}$ ergibt sich für die Gaußverteilung (englisch: Gaussian PDF) unabhängig vom Mittelwert $m_1$:
$$h_{\rm max}(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.1cm} \rm L} \cdot \sigma^2) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm L} = 2\pi{\rm e} \hspace{0.05cm}.$$
Jede andere wertkontinuierliche Zufallsgröße $X$ mit Varianz ${\rm E}[|X – m_1|^2] ≤ σ^2$ führt zu einer kleineren differentiellen Entropie, gekennzeichnet durch die Kenngröße $Γ_L < 2πe$.
