Exercise 4.8: Numerical Analysis of the AWGN Channel Capacity

Kapazität C für gegebenes E_S/N₀

Für die Kanalkapazität$C$ des AWGN–Kanals als obere Schranke für die Coderate $R$ bei Digitalsignalübertragung gibt es zwei verschiedene Gleichungen:

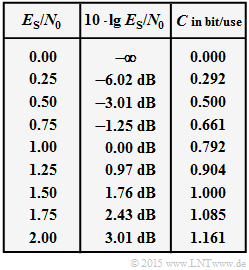
Kanalkapazität C in Abhängigkeit der Energie pro Symbol:

$$C( E_{\rm S}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot E_{\rm S}}{N_0}) .$$

Hierbei sind folgende Abkürzungen verwendet:

$E_{\rm S}$ bezeichnet die (mittlere) Energie pro Symbol des Digitalsignals,
$N_0$ gibt die AWGN–Rauschleistungsdichte an.

Kanalkapazität C in Abhängigkeit der Energie pro Bit:

$$C( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) .$$

Zu berücksichtigen ist der Zusammenhang $E_{\rm S} = R \cdot E_{\rm B}$, wobei $R$ die Coderate der bestmöglichen Kanalcodierung angibt.
Eine fehlerfreie Übertragung (unter Berücksichtigung dieses optimalen Codes) ist für das gegebene $E_{\rm B}/N_0$ möglich, so lange $R \le C$ gilt ⇒ Kanalcodierungstheorem von Shannon.

Durch die Tabelle vorgegeben ist der Kurvenverlauf der Kanalkapazität in Abhängigkeit von $E_{\rm S}/N_0$. Im Mittelpunkt dieser Aufgabe steht die numerische Auswertung der zweiten Gleichung.

Hinweise:

Die Aufgabe gehört zum Kapitel AWGN–Kanalkapazität bei wertkontinuierlichem Eingang.
Bezug genommen wird insbesondere auf die Seiten Die Kanalkapazität C als Funktion von E_S/N₀ sowie Die Kanalkapazität C als Funktion von E_B/N₀
Da die Ergebnisse in „bit” angegeben werden sollen, wird in den Gleichungen „log” ⇒ „log₂” verwendet.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

	Es gilt: $R = 1/2 \cdot \log_2 (1 + 2 \cdot R \cdot E_{\rm B}/{N_0})$.
	Es gilt: $2^{2R} = 1 + 2 \cdot R \cdot E_{\rm B}/{N_0}$.
	Es gilt: $E_{\rm B}/{N_0} = (2^{2R} -1)/(2R) $.

$\text{Min} \ [E_{\rm B}/{N_0}] \ = \ $

$\text{Min} \ [10 \cdot \lg (E_{\rm B}/{N_0})] \ = \ $

$ \ \rm dB$

$C \ = \ $

$ \ \rm bit/Kanalzugriff$

$\text{Min} \ [E_{\rm B}/{N_0}] \ = \ $

	Berechnung der Kanalkapazität $C$ für das vorgegebene $E_{\rm B}/{N_0}$.
	Berechnung des erforderlichen $E_{\rm B}/{N_0}$ für das vorgegebene $C$.

Musterlösung

Solution

(1) Ausgehend von der Gleichung $$C = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + { 2 \cdot E_{\rm S}}/{N_0}) $$ erhält man mit C = R und E_S = R · E_B die Gleichung gemäß Lösungsvorschlag 1: $$R = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + { 2 \cdot R \cdot E_{\rm B}}/{N_0})\hspace{0.05cm}. $$ Bringt man den Faktor 1/2 auf die linke Seite der Gleichung und bildet die Potenz zur Basis 2, so erhält man den Lösungsvorschlag 2: $$2^{2R} = 1 + 2 \cdot R \cdot E_{\rm B}/{N_0}\hspace{0.05cm}. $$ Löst man diese Gleichung nach E_B/N₀ auf, so ergibt sich $$E_{\rm B}/{N_0} = \frac{2^{2R} - 1} { 2 R} \hspace{0.05cm}. $$ Das bedeutet: Alle Lösungsvorschläge sind richtig.

(2) Über einen Kanal mit der Kanalkapazität C ist eine fehlerfreie Übertragung möglich, solange die Coderate R ≤ C ist. Die absolute Grenze ergibt sich im Grenzfall C = R = 0. Oder präziser ausgedrückt: für ein beliebig kleines positives ε: C = R = ε mit ε → 0.

Mit dem Ergebnis der Teilaufgabe (a) lautet die Bestimmungsgleichung: $${\rm Min}\hspace{0.1cm}[E_{\rm B}/{N_0}] = \lim\limits_{R \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}\frac{2^{2R} - 1} { 2 R} \hspace{0.05cm}. $$ Da hier der Quotient im Grenzübergang R → 0 das Ergebnis „0 geteilt durch 0” liefert, ist hier die l'Hospitalsche Regel anzuwenden: Man differenziert Zähler und Nenner, bildet den Quotienten und setzt schließlich R = 0 ein. Mit x = 2R lautet das Ergebnis: $${\rm Min}\hspace{0.1cm}[E_{\rm B}/{N_0}] = \lim\limits_{x \hspace{0.05cm}\rightarrow \hspace{0.05cm}0}\frac{2^{x} - 1} { x} = \frac{{\rm ln}\hspace{0.1cm} (2) \cdot 2^{x} } { 1} \hspace{0.05cm}\bigg |_{x=0} = {\rm ln}\hspace{0.1cm} (2) \hspace{0.15cm}\underline{= 0.693} \hspace{0.05cm}.$$

(3) In logarithmierter Form erhält man: $${\rm Min}\hspace{0.1cm}[10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0})] = 10\cdot {\rm lg} \hspace{0.1cm}(0.693) \hspace{0.15cm}\underline{= -1.59\,{\rm dB}} \hspace{0.05cm}. $$

(4) Der Abszissenwert lautet somit in nichtlogarithmierter Form: E_B/N₀ = 1. Daraus folgt mit C = R: $$\frac{2^{2C} - 1} { 2 C} \stackrel{!}{=} 1 \hspace{0.3cm}\Rightarrow\hspace{0.3cm}\underline{C = 0.5} \hspace{0.05cm}. $$

(5) Für R = 1 ist E_B = E_S. Deshalb gilt: $$ C(E_{\rm B}/{N_0}) = 1 \hspace{0.3cm}\Longleftrightarrow \hspace{0.3cm} C(E_{\rm S}/{N_0}) = 1 \hspace{0.05cm}.$$ Aus der Tabelle auf der Angabenseite ist abzulesen: $$ C(E_{\rm S}/{N_0}) = 1 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} E_{\rm S}/{N_0} = 1.5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \underline{E_{\rm B}/{N_0} = 1.5}\hspace{0.05cm}.$$ Der dazugehörige dB–Wert ist 10 · lg (E_B/N₀) = 1.76 dB.

Zum gleichen Ergebnis kommt man mit R = 1 über die Gleichung $$E_{\rm B}/{N_0} = \frac{2^{2R} - 1} { 2 \cdot R} = \frac{4 - 1} { 2 } = 1.5 \hspace{0.05cm}.$$ (6) Richtig ist der Lösungsvorschlag 2, wie an einem Beispiel gezeigt werden soll.

Gesucht ist die Kanalkapazität C für 10 · lg (E_B/N₀) = 15 dB ⇒ E_B/N₀ = 31.62. Dann gilt entsprechend dem Lösungsvorschlag 1 mit x = 2C:

$$31.62 = \frac{2^{x} - 1} { x} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 31.62 \cdot x = 2^{x} - 1 \hspace{0.05cm}. $$

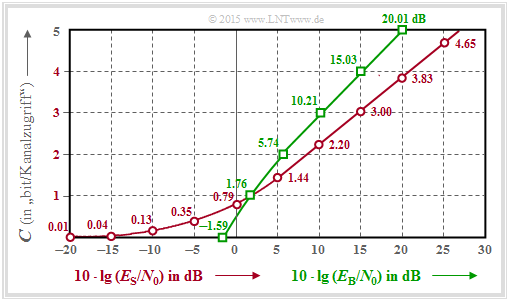
Die Lösung x = 7.986 ⇒ C = 3.993 (bit/use) kann nur grafisch oder iterativ gefunden werden.

Gesucht ist der notwendige Abszissenwert 10 · lg (E_B/N₀) für die Kapazität C = 4 bit/Symbol:

$$E_{\rm B}/{N_0} = \frac{2^{2C} - 1} { 2 \cdot C} = \frac{2^8 - 1} { 8 } = 31.875 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0}) = 15.03\,{\rm dB} \hspace{0.05cm}.$$

Die Grafik zeigt die AWGN–Kanalkapazität C in „bit/Kanalzugriff” oder auch „bit/Symbol” abhängig von

10 · lg (E_S/N₀) ⇒ rote Kurve und rote Zahlen;
diese

geben die Kanalkapazität C für das vorgegebene 10 · lg (E_S/N₀) an.

10 · lg (E_B/N₀) ⇒ grüne Kurve und und grüne Zahlen;
diese geben das erforderliche 10 · lg (E_B/N₀) für die vorgegebene Kanalkapazität C an.

Der Schnittpunkt der beiden Kurven liegt bei 1.76 dB.