Exercise 2.2: Modulation Depth

• Return to book

Modulationsgrad-Definition bei ZSB–AM

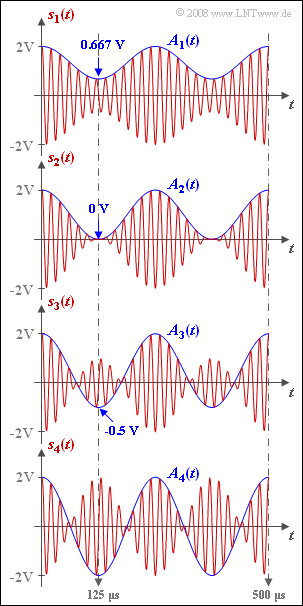
Die Grafik zeigt ZSB–amplitudenmodulierte Signale $s_1(t)$ bis $s_4(t)$ mit unterschiedlichem Modulationsgrad $m$. Nachrichtensignal $q(t)$ und Trägersignal $z(t)$ seien jeweils cosinusförmig:

$$q(t) = A_{\rm N} \cdot \cos (2 \pi f_{\rm N} t),\hspace{0.2cm} f_{\rm N} = 4\,{\rm kHz}\hspace{0.05cm},$$

$$ z(t) = \hspace{0.2cm}1 \hspace{0.15cm} \cdot \cos (2 \pi f_{\rm T} t),\hspace{0.2cm} f_{\rm T} = 50\,{\rm kHz}\hspace{0.05cm}.$$

Das modulierte Signal (Sendesignal) lautet mit dem im Modulator zugesetzten Gleichanteil $A_{\rm T}$:

$$s(t ) = A(t) \cdot z(t), \hspace{0.2cm} A(t) = q(t) + A_{\rm T}\hspace{0.05cm}.$$

Bei den Grafiken wurde zur Normierung gewählt:

$$A_{\rm T}+ A_{\rm N} = 2\,{\rm V}\hspace{0.05cm}.$$

• Ist der Modulationsgrad $m ≤ 1$, so ist $A(t)= q(t) + A_{\rm T}$ gleich der Hüllkurve $a(t)$.
• Dagegen gilt für den Modulationsgrad $m > 1$:

$$a(t ) = |A(t)|\hspace{0.05cm}.$$

Der cosinusförmige Verlauf $A(t)$ schwankt zwischen $A_{\rm max}$ und $A_{\rm min}$, wobei wegen der obigen Normierung stets $A_{\rm max} = 2 \ \rm V$ ist. Die Minimalwerte von $A(t)$ treten zum Beispiel bei der halben Periodendauer des Quellensignals (also für $t = 125 \ \rm μs$) auf:

$$A_{\rm min} = q(T_0/2)+ A_{\rm T} = A_{\rm T}-A_{\rm N}.$$

Die Zahlenwerte sind in der Grafik angegeben.

Hinweise:

• Die Aufgabe gehört zum Kapitel Zweiseitenband-Amplitudenmodulation.
• Bezug genommen wird insbesondere auf die Seite ZSB-Amplitudenmodulation mit Träger.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Bestimmen Sie für die Signale $s_1(t)$, $s_2(t)$, $s_3(t)$ jeweils den Modulationsgrad.

$m_1 \ = \ $

$m_2 \ = \ $

$m_3 \ = \ $

2

Welche Aussagen treffen für das Signal $s_4(t)$ zu?

	Es handelt sich um „ZSB–AM ohne Träger”.
	Der Modulationsgrad ist $m = 0$.
	Der Modulationsgrad $m$ ist unendlich groß.

3

Es gelte nun $A_{\rm T} = A_{\rm N} = 1\ \rm V$, also $m = 1$. Wie lautet das Spektrum $S_+(f)$ des analytischen Signals?
Welche Diracgewichte treten bei $f_{\rm T}$ sowie bei $f_{\rm T}± f_{\rm N}$ auf?

$S_+(f_{\rm T}) \ = \ $ $\ \text{V}$

$S_+(f_{\rm T} ± f_{\rm N}) \ = \ $ $\ \text{V}$

4

Es gelte weiter $m = 1$. Welcher Anteil $P_{\rm T}/P_{\rm S}$ der gesamten Sendeleistung $P_{\rm S}$ geht allein auf den Träger zurück, der nicht zur Demodulation genutzt werden kann?

$P_{\rm T}/P_{\rm S} \ = \ $

5

Verallgemeinern Sie das Ergebnis aus (4) für einen beliebigen Modulationsgrad $m$. Welche Leistungsverhältnisse ergeben sich für $m = 0.5$, $m = 3$ und $m → ∞$ ?

$m = 0.5\text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $

$m = 3.0\text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $

$m → ∞ \text{:}\hspace{0.3cm} P_{\rm T}/P_{\rm S} \ = \ $

6

Welche der nachfolgenden Bewertungen erscheinen Ihnen nach den bisherigen Berechnungen als sinnvoll?

	$m ≈ 1$ ist aus energetischen Gründen günstiger als ein kleines $m$.
	Nur bei Hüllkurvendemodulation ist der Träger sinnvoll.

Musterlösung

Solution

1.Aus den beiden Gleichungen $$ A_{\rm max} = A_{\rm T}+A_{\rm N}=2\,\,{\rm V},\hspace{0.3cm} A_{\rm min} = A_{\rm T}-A_{\rm N}\hspace{0.05cm}$$ folgt direkt $$A_{\rm N} = (A_{\rm max} - A_{\rm min})/2$$ $$A_{\rm T} = (A_{\rm max} + A_{\rm min})/2\hspace{0.05cm}.$$ Somit lautet der Modulationsgrad $$m = \frac{A_{\rm max} - A_{\rm min}}{A_{\rm max} + A_{\rm min}}\hspace{0.05cm}.$$ Mit den angegebenen Zahlenwerten erhält man: $$ m_1 = \frac{2\,{\rm V} - 0.667\,{\rm V}}{2\,{\rm V} + 0.667\,{\rm V}} \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}, \hspace{0.5cm} m_2 = \frac{2\,{\rm V} - 0\,{\rm V}}{2\,{\rm V} + 0\,{\rm V}} \hspace{0.15cm}$$ $$m_3 = \frac{2V - (-1)}{2V - (-1)} \underline{=3.0}$$

2. In diesem Fall ist $A_T = 0$, das heißt, es liegt tatsächlich eine „ZSB–AM ohne Träger” vor und der Modulationsgrad $m = A_N/A_T$ ist unendlich groß. Richtig sind demnach die Aussagen 1 und 3.

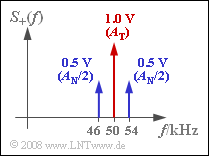
3.Das Spektrum $S_+(f)$ setzt sich für jeden Modulationsgrad m aus drei Diraclinien mit den Gewichten $A_T$ (bei $f = f_T$) sowie $m/2 · A_T$ (bei $f = f_T ± f_N$) zusammen. Für m = 1 ergeben sich die Gewichte entsprechend der Skizze: $S_+(f_T) = 1V$, $S_+(f_T ± f_N) = 0.5V$.

4. Die auf den Widerstand 1 Ω bezogene Leistung (Quadrat des Effektivwertes) einer harmonischen Schwingung mit der Amplitude $A_T$ beträgt (mit $A_T = 1V$): $$P_{\rm T} ={A_{\rm T}^2}/{2} = 0.5\,{\rm V}^2 \hspace{0.05cm}.$$ In gleicher Weise erhält man für die Leistungen des unteren und des oberen Seitenbandes: $$P_{\rm USB} = P_{\rm OSB} =({A_{\rm N}}/{2})^2/2 = 0.125\,{\rm V}^2 \hspace{0.05cm}.$$ Das gesuchte Verhältnis ist somit: $$m=1: \hspace{0.15cm} \frac{P_{\rm T}}{P_{\rm S}}= \frac{P_{\rm T}}{P_{\rm USB} + P_{\rm T}+ P_{\rm OSB}}= \frac{0.5\,{\rm V}^2}{0.125\,{\rm V}^2 + 0.5\,{\rm V}^2+ 0.125\,{\rm V}^2}= 2/3\hspace{0.15cm}\underline { = 0.667}\hspace{0.05cm}.$$

5. Mit den Diracgewichten $m/2 · A_T$ der beiden Seitenbänder (siehe Erklärungen unter c) erhält man $$\frac{P_{\rm T}}{P_{\rm S}}= \frac{A_{\rm T}^2/2}{A_{\rm T}^2/2 + 2 \cdot (m/2)^2 \cdot A_{\rm T}^2/2}= \frac{2}{2 + m^2}\hspace{0.05cm}.$$ Dies führt zu den Zahlenwerten 8/9 = 0.889 (für m = 0.5), 2/11 = 0.182 (für m = 3) und 0 (für m → ∞).

6.Die Zusetzung des Trägers macht nur Sinn, um den einfacheren Hüllkurvendemodulator verwenden zu können. Dies geht nur für m < 1. Ist dagegen der Modulationsgrad größer als 1 und somit der Einsatz eines Synchrondemodulators erforderlich, sollte man aus energetischen Gründen auf den Träger (fast) ganz verzichten. Ebenso ist bei Anwendung eines Hüllkurvendemodulators aus energetischen Gründen ein möglichst großer Modulationsgrad m < 1 anzustreben. Beide Aussagen treffen also zu.

Allerdings kann durch einen kleinen Restträger die Trägerrückgewinnung erleichtert werden, die beim Synchrondemodulator zur Frequenz- und Phasensynchronisation benötigt wird. Die zweite Aussage ist somit nur bedingt als richtig zu bewerten.