Aufgaben:Aufgabe 2.11Z: Nochmals ESB-AM & Hüllkurvendemodulation

• Return to book

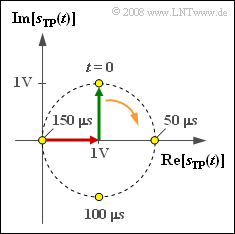
Nebenstehende Grafik zeigt die Ortskurve – also die Darstellung des äquivalenten TP–Signals in der komplexen Ebene – für ein ESB–AM–System.

Weiter ist bekannt, dass die Trägerfrequenz $f_T = 100 kHz$ beträgt und dass der Kanal ideal ist: $$r(t) = s(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} r_{\rm TP}(t) = s_{\rm TP}(t) \hspace{0.05cm}.$$

Beim Empfänger wird ein idealer Hüllkurvendemodulator (HKD) eingesetzt. Im Verlauf dieser Aufgabe werden folgende Größen benutzt:

• das Seitenband–zu–Träger–Verhältnis

$$\mu = \frac{A_{\rm N}/2}{A_{\rm T}}\hspace{0.05cm},$$

• die Hüllkurve

$$a(t) = |s_{\rm TP}(t)| \hspace{0.05cm},$$

• die maximale Abweichung $τ_{max}$ der Nulldurchgänge von $s(t)$ und Trägersignal $z(t)$.

Hinweis: Die Aufgabe bezieht sich auf den Theorieteil von Kapitel 2.4. Für diese Aufgabe gelten vergleichbare Voraussetzungen wie für die Aufgabe A2.10.

Fragebogen

1

Geben Sie das äquivalente TP–Signal in analytischer Form an und beantworten Sie folgende Fragen.

	Es handelt sich um eine OSB–AM.
	Es handelt sich um eine USB–AM.
	Das Nachrichtensignal $q(t)$ ist cosinusförmig.
	Das Nachrichtensignal $q(t)$ ist sinusförmig.

2

Geben Sie die Amplitude und Frequenz des Quellensignals an. Berücksichtigen Sie, dass es sich um eine ESB–AM handelt.

$A_N$ = $V$

$f_N$ = $KHz$

3

Welcher Wert ergibt sich für das sog. Seitenband–zu–Träger–Verhältnis $μ$? Verwenden Sie diese Größe zur Beschreibung von $s_{TP}(t)$.

$μ$ =

4

Berechnen Sie den zeitlichen Verlauf der Hüllkurve $a(t)$. Welche Werte treten bei $t = 50 μs$, $t = 100 μs$ und $t = 150 μs$ auf?

$a(t = 50 μs)$ = $V$

$a(t = 100 μs)$ = $V$

$a(t = 150 μs)$ = $V$

5

Um welche Zeitdifferenz τmax (betragsmäßig) sind die Nulldurchgänge von $s(t)$ gegenüber $z(t)$ maximal verschoben?

$τ_{max}$ = $μs$

Musterlösung

Solution

1.Richtig sind die Lösungsvorschläge 2 und 4. Das äquivalente TP–Signal lautet: $$s_{\rm TP}(t) = 1\,{\rm V} + {\rm j}\cdot 1\,{\rm V}\cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \hspace{0.05cm}.$$ Die Ortskurve ist ein Kreis mit dem Mittelpunkt bei $A_T = 1 V$. Da die Drehung im Uhrzeigersinn erfolgt, handelt es sich um eine USB–AM. Der sich drehende (grüne) Zeiger zeigt zum Starzeitpunkt $t = 0$ in Richtung der imaginären Achse. Daraus folgt, dass für das Quellensignal gelten wird: $$q(t) = A_{\rm N} \cdot \sin(\omega_{\rm N} \cdot t).$$

2. Bei der USB wird nur das untere Seitenband mit der Zeigerlänge $A_N/2 = 1 V$ übertragen. Daraus ergibt sich $A_N = 2 V$. Für eine Umdrehung in der Ortskurve benötigt der Zeiger die Zeit $200 μs$. Der Kehrwert hiervon ist die Frequenz $f_N = 5 kHz$.

3. Entsprechend der Definition auf der Angabenseite und den Ergebnissen zu a) und b) gilt: $$\mu = \frac{A_{\rm N}/2}{A_{\rm T}}=1\hspace{0.05cm}.$$ Damit kann für das äquivalente TP–Signal auch geschrieben werden: $$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + {\rm j} \cdot \mu \cdot {\rm e}^{-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm}\omega_{\rm N}\cdot \hspace{0.03cm}\hspace{0.03cm}t} \right),\hspace{0.3cm}{\rm hier}\hspace{0.15cm}\mu \hspace{0.15cm}\underline {= 1} \hspace{0.05cm}.$$

4.Spaltet man die komplexe Exponentialfunktion mit dem Satz von Euler nach Real– und Imaginärteil auf, so erhält man: $$s_{\rm TP}(t) = A_{\rm T} \cdot \left( 1 + \sin(\omega_{\rm N}\cdot t) + {\rm j} \cos(\omega_{\rm N}\cdot t)\right) \hspace{0.05cm}.$$

Durch Anwendung des Satzes von Pythagoras kann hierfür auch geschrieben werden: $$a(t) = |s_{\rm TP}(t)| = A_{\rm T} \cdot \sqrt{ (1 + \sin(\omega_{\rm N}\cdot t))^2 + \cos^2(\omega_{\rm N}\cdot t)} =$$ $$= |s_{\rm TP}(t)| = A_{\rm T} \cdot \sqrt{ 2 + 2 \cdot \sin(2\omega_{\rm N}\cdot t)} \hspace{0.05cm}.$$ Die abgefragten Werte lauten mit $A_T = 1 V$: $$a(t = 50\,{\rm \mu s}) \hspace{0.15cm}\underline {= 2\,{\rm V}},\hspace{0.3cm}a(t = 100\,{\rm \mu s}) \hspace{0.15cm}\underline {= 1.414\,{\rm V}},\hspace{0.3cm}a(t = 150\,{\rm \mu s}) \hspace{0.15cm}\underline {= 0} \hspace{0.05cm}.$$ Diese Ergebnisse können auch direkt aus der Grafik auf der Angabenseite abgelesen werden. 5.Ein Hinweis für die Lage der Nulldurchgänge von $s(t)$ gegenüber dem durch das Trägersignal $z(t)$ vorgegebenen Raster liefert die Phasenfunktion $ϕ(t)$. Bei der gegebenen Ortskurve können diese Werte zwischen $±π/2 (±90°)$ annehmen. Diese Maximalwerte treten zum Beispiel im Bereich um $t ≈ 150 μs$ auf, da hier ein Phasensprung stattfindet. Der Zusammenhang zwischen $τ_{max}$ und $ϕ_{max}$ lautet: $$\tau_{\rm max} = \frac {\Delta \phi_{\rm max}}{2 \pi }\cdot \frac{1 }{f_{\rm T}} = \frac {1}{4}\cdot 10\,{\rm \mu s} \hspace{0.15cm}\underline {= 2.5\,{\rm \mu s}} \hspace{0.05cm}.$$