Exercise 3.10: Noise Power Calculation

• Return to book

Rauschleistungsdichten von PM und FM

Betrachtet werden die Phasen– und Frequenzmodulation einer Cosinusschwingung mit der Frequenz $f_{\rm N}$. Zunächst gelte für die Nachrichtenfrequenz $f_{\rm N} = f_5 = 5 \ \rm kHz$ und der Modulationsindex (Phasenhub) sei $η = 5$.

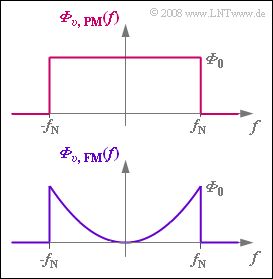
Bei Vorhandensein von additivem Gaußschen Rauschen mit der Rauschleistungsdichte $N_0$ ergibt sich nach dem PM–Demodulator eine konstante Rauschleistungsdichte ${\it \Phi}_{υ, PM}(f) = {\it \Phi}_0$, die auch vom Modulationsindex abhängt:

$${\it \Phi}_0 = \frac{N_0}{\eta^2} \hspace{0.05cm}.$$

Für die Berechnung der Rauschleistung $P_{\rm R}$ ist lediglich der Frequenzbereich von $±f_{\rm N}$ relevant (siehe Grafik).

Die Rauschleistungsdichte nach der FM–Demodulation lautet mit dem Frequenzhub $Δf_{\rm A}$:

$${\it \Phi}_{v {\rm , \hspace{0.08cm}FM} } (f) = N_0 \cdot \left(\frac{f}{\Delta f_{\rm A}}\right)^2 \hspace{0.05cm}.$$

• Gegeben ist der Rauschabstand $10 · \lg ρ_v = 50 \ \rm dB$ für Phasenmodulation und $f_N = 5 kHz$.
• Gesucht sind in dieser Aufgabe der Rauschabstand bei FM für die Nachrichtenfrequenz $f_{\rm N} = 5 \ \rm kHz$) sowie die sich ergebenden Rauschabstände von PM und FM für die Nachrichtenfrequenz $f_{\rm N} = f_{10} = 10 \ \rm kHz$.

Hinweise:

• Die Aufgabe gehört zum Kapitel Rauscheinfluss bei Winkelmodulation.
• Bezug genommen wird aber auch auf das Kapitel Phasenmodulation und insbesondere auf den Abschnitt Signalverläufe bei Frequenzmodulation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Gehen Sie bei der Berechnung von folgenden Werten der Besselfunktion aus:

$${\rm J}_0 (2.4) \approx 0, \hspace{0.2cm}{\rm J}_1 (2.4) = -{\rm J}_{-1} (2.4)\approx 0.52, \hspace{0.2cm}{\rm J}_2 (2.4) = {\rm J}_{-2} (2.4)\approx 0.43.$$

Hinweis: Diese Aufgabe bezieht sich auf den Theorieteil von Kapitel 3.3.

Fragebogen

1

Welcher Rauschabstand ergibt sich bei $f_N = 10 kHz$ und PM? Interpretieren Sie das Ergebnis.

$PM, f_N = 10 kHz: 10 · lg ρ_υ$ = $dB$

2

Berechnen Sie den Rauschabstand für $f_N = 5 kHz$ und FM. Wie groß ist der Modulationsindex bei dieser Konstellation?

$FM, f_N = 5 kHz: 10 · lg ρ_υ$ = $dB$

3

Berechnen Sie den Rauschabstand für $f_N = 10 kHz$ und FM. Interpretieren Sie das Ergebnis im Vergleich zu den Teilfragen a) und b).

$ FM, f_N = 10 kHz: 10 · lg ρ_υ$ = $KHz$

Musterlösung

Solution

1. Das Signal–zu–Rausch–Leistungsverhältnis (Sinken–SNR) ρυ ist der Quotient aus der Nutzleistung $P_S$ und der Rauschleistung $P_R$. Speziell bei der Phasenmodulation gilt: $$ \rho_{v } = \frac{P_{\rm S}}{P_{\rm R}} = \frac{P_{\rm S}}{{\it \Phi}_0 \cdot 2 f_{\rm N} } =\frac{\eta^2}{2} \cdot \frac{P_{\rm S}}{N_0 \cdot f_{\rm N} }\hspace{0.05cm}.$$ Die Messung mit $f_N = f_5 = 5 kHz$ hat das SNR $ρ_υ = 105$ (entsprechend $50 dB$) ergeben. Die doppelte Nachrichtenfrequenz führt zum halben SNR, da nun die doppelte Rauschleistung wirksam ist: $$ \rho_{v }= 0.5 \cdot 10^5 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}\underline {\approx 46.99\,{\rm dB}}\hspace{0.05cm}.$$ Dieses Ergebnis lässt sich auch über die Beziehung $ρ_υ = η^2/2 · ξ$ herleiten. Bei PM ist η unabhängig von der Nachrichtenfrequenz. Der SNR–Verlust geht darauf zurück, dass nun $ξ = P_S/(N_0 · f_N)$ halbiert wird.

2. Bei Frequenzmodulation und der Nachrichtenfrequenz $f_N = 5 kHz$ erhält man für die Rauschleist $$P_{\rm R} = \int_{-f_{\rm N}}^{ + f_{\rm N}} {\it \Phi}_{v {\rm , \hspace{0.08cm}FM} } (f)\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0}{\Delta f_{\rm A}^{\hspace{0.1cm}2}} \cdot \int_{0}^{ f_{\rm N}} f^2\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0 \cdot f_{\rm N}^{\hspace{0.1cm}3}}{3 \cdot \Delta f_{\rm A}^2} \hspace{0.05cm}.$$ Unter Berücksichtigung von $Δf_A = η · f_N$ (Frequenzhub) ergibt sich somit: $$P_{\rm R} = \frac{2 \cdot N_0 \cdot f_{\rm N}}{3 \cdot \eta^2} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \rho_{v }= \frac{3 \cdot \eta^2 \cdot P_{\rm S}}{2 \cdot N_0 \cdot f_{\rm N}} = 3 \cdot \rho_{v {\rm , \hspace{0.08cm}PM}}\hspace{0.05cm}.$$ Das heißt: Die Frequenzmodulation ist um den Faktor 3 (oder 4.77 dB) besser als die PM: $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }= 50\,{\rm dB} + 10 \cdot {\rm lg} \hspace{0.15cm}{3}\hspace{0.15cm}\underline {\approx 54.77\,{\rm dB}}\hspace{0.05cm}.$$

3. Entsprechend dem Ergebnis aus b) erhält man mit $f_{10} = 10 kHz$: $$P_{\rm R} = \frac{2 \cdot N_0 \cdot f_{\rm 10}}{3 \cdot \eta_{10}^{\hspace{0.1cm}2}} = \frac{ f_{\rm 10} \cdot \eta_{5}^{\hspace{0.1cm}2}}{ 3 \cdot f_{\rm 5} \cdot \eta_{10}^{\hspace{0.1cm}2}}\cdot \frac{2 \cdot N_0 \cdot f_{\rm 5}}{\eta_{5}^{\hspace{0.1cm}2}} \hspace{0.05cm}.$$ Der zweite Term gibt die Rauschleistung des Vergleichssystems (Phasenmodulation, $f_N = f_5$) an, die zum Ergebnis $10 · lg ρ_υ = 50 dB$ geführt hat.

Bei FM ist nun jedoch der Modulationsindex umgekehrt proportional zur Nachrichtenfrequenz, so dass der Quotient $η_5^2/η_{10}^2 = 4$ ist. Somit ergibt sich für den Vorfaktor 8/3. Aufgrund der größeren Rauschleistung ist das SNR kleiner: $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v }= 50\,{\rm dB} - 10 \cdot {\rm lg} \hspace{0.15cm}({8}/{3})\hspace{0.15cm}\underline {\approx 45.74\,{\rm dB}}\hspace{0.05cm}.$$ Bei gleicher Nachrichtenfrequenz $f_N = 10 kHz$ ist nun die FM um 1.25 dB schlechter als die PM, da sich nun die Halbierung von η – nach Quadrierung der Faktor 4 – stärker auswirkt als der systembedingte Faktor 3, um den die FM gegenüber der PM überlegen ist.

Der Vergleich der Teilaufgaben b) und c) zeigt einen Unterschied um den Faktor 8 bzw. 9.03 dB. Der ungünstigere Wert für die größere Nachrichtenfrequenz $f_N = 10 kHz$ ergibt sich durch den nur halb so großen Modulationsindex – nach Quadrierung Faktor 4 – und die doppelte Rauschbandbreite.