Exercise 4.16: Comparison between Binary PSK and Binary FSK

• Return to book

Fehlerwahrscheinlichkeit von BPSK und BFSK

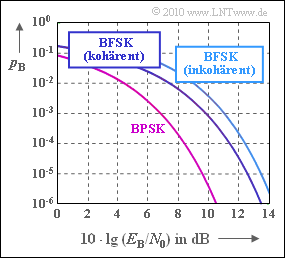
Die Grafik zeigt die Bitfehlerwahrscheinlichkeit für eine binäre FSK–Modulation bei

• kohärenter Demodulation bzw.
• inkohärenter Demodulation

im Vergleich zur binären Phasenmodulation (BPSK).

Es wird stets Orthogonalität vorausgesetzt. Bei kohärenter Demodulation kann hierbei der Modulationsindex ein Vielfaches von $h = 0.5$ sein, so dass die mittlere Kurve auch für Minimum Shift Keying (MSK) gültig ist. Dagegen muss bei nichtkohärenter Demodulation einer FSK der Modulationsindex ein Vielfaches von $h = 1$ sein.

Diesem Systemvergleich liegt wieder der AWGN–Kanal zugrunde, gekennzeichnet durch das Verhältnis $E_{\rm B}/N_0$. Die Gleichungen für die Bitfehlerwahrscheinlichkeiten lauten bei

• Binary Phase Shift Keying (BPSK):

$$p_{\rm B} = {\rm Q}\left ( \sqrt{\frac{2 \cdot E_{\rm B}}{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ),$$

• Binary Frequency Shift Keying (BFSK) mit kohärenter Demodulation:

$$p_{\rm B} = {\rm Q}\left ( \sqrt{{E_{\rm B}}/{N_0 }} \hspace{0.1cm}\right ) = {1}/{2}\cdot {\rm erfc}\left ( \sqrt{\frac{E_{\rm B}}{2 \cdot N_0 }} \hspace{0.1cm}\right ),$$

• Binary Frequency Shift Keying (BFSK) mit inkohärenter Demodulation:

$$p_{\rm B} = {1}/{2} \cdot {\rm e}^{- E_{\rm B}/{(2N_0) }}\hspace{0.05cm}.$$

In Aufgabe 4.8 wurde gezeigt, dass bei der BPSK das logarithmierte Verhältnis $10 · \lg \ E_{\rm B}/N_0$ mindestens $9.6 \ \rm dB$ betragen muss, damit die Bitfehlerwahrscheinlichkeit den Wert $p_{\rm B} = 10^{–5}$ nicht überschreitet.

Hinweise:

• Die Aufgabe gehört zum Kapitel Nichtlineare digitale Modulation.
• Bezug genommen wird aber auch auf das Kapitel Lineare digitale Modulation.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
• Verwenden Sie die Näherung $\lg(2) ≈ 0.3$.

Fragebogen

1

Welches $E_B/N_0$ ist bei MSK und kohärenter Demodulation erforderlich, damit $p_B ≤ 10^{–5}$ erfüllt ist?

$MSK, \text{kohärent}: 10 · lg E_B/N_0$ = $dB$

2

Sind folgende Aussagen richtig: Das gleiche Ergebnis erhält man bei

	einer FSK mit Modulationsindex $η = 0.7$,
	einer FSK mit Modulationsindex $η = 1$?

3

Welches $E_B/N_0$ ist bei FSK mit dem Modulationsindex h = 1 und inkohärenter Demodulation erforderlich, damit $p_B ≤ 10^{–5}$ erfüllt ist?

$FSK, \text{inkohärent}: 10 · lg E_B/N_0$ = $dB$

4

Welche Fehlerwahrscheinlichkeit ergibt sich bei $10 · lg E_B/N_0 = 12.6 dB$ und inkohärenter Demodulation?

$FSK, \text{inkohärent}: p_B$ = $10^{-4}$

Musterlösung

Solution

1. Ein Vergleich der beiden ersten Gleichungen auf der Angabenseite macht deutlich, dass bei der MSK mit kohärenter Demodulation das AWGN–Verhältnis $E_B/N_0$ verdoppelt werden muss, damit die gleiche Fehlerwahrscheinlichkeit wie bei BPSK erreicht wird. In anderen Worten: Die kohärente BFSK–Kurve liegt um $10 · lg (2) ≈ 3 dB$ rechts von der BPSK–Kurve. Um $p_B ≤ 10^{–5}$ zu garantieren, muss gelten: $$10 \cdot {\rm lg}\hspace{0.05cm}{E_{\rm B}} /{N_{\rm 0}}= 9.6\,\,{\rm dB} + 3\,\,{\rm dB} = \underline{12.6\,\,{\rm dB}}\hspace{0.05cm}.$$

2. Die angegebene Gleichung gilt nicht nur für die MSK (diese ist eine FSK mit $η = 0.5$), sondern für jede Form von orthogonaler FSK. Eine solche liegt vor, wenn der Modulationsindex η ein ganzzahliges Vielfaches von 0.5 ist, zum Beispiel für $η = 1$. Mit $η = 0.7$ ergibt sich keine orthogonale FSK. Es kann gezeigt werden, dass sich für $η = 0.7$ sogar eine kleinere Fehlerwahrscheinlichkeit als bei orthogonaler FSK ergibt. Mit $10 · lg E_B/N_0 = 12.6 dB$ erreicht man hier sogar $p_B ≈ 10^{–6}$, also eine Verbesserung um eine Zehnerpotenz. Richtig ist demzufolge der Lösungsvorschlag 2.

3. Aus der Umkehrfunktion der angegebenen Gleichung erhält man: $$\frac{E_{\rm B}} {2 \cdot N_{\rm 0}}= {\rm ln}\hspace{0.05cm}\frac{1}{2 p_{\rm B}}= {\rm ln}(50000)\approx 10.82$$ $$\Rightarrow \hspace{0.3cm}{E_{\rm B}} /{N_{\rm 0}}= 21.64 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.05cm}{E_{\rm B}}/ {N_{\rm 0}}\approx \underline{13.4\,\,{\rm dB}}\hspace{0.05cm}.$$

4. Aus $10 · lg E_B/N_0 = 12.6 dB$ folgt: $${E_{\rm B}} /{N_{\rm 0}}= 10^{1.26} \approx 16.8 \hspace{0.25cm}\Rightarrow \hspace{0.25cm} ({E_{\rm B}} /{N_{\rm 0}})/2 \approx 8.4 \hspace{0.25cm} \Rightarrow \hspace{0.25cm} p_{\rm B} = {1}/{2} \cdot {\rm e}^{- 8.4} \approx \underline{1.12 \cdot 10^{-4}}\hspace{0.05cm}.$$ Das heißt: Bei gleichem $E_B/N_0$ wird die Fehlerwahrscheinlichkeit bei der inkohärenten Demodulation gegenüber kohärenter Demodulation (siehe Teilaufgabe a) um etwa den Faktor 11 vergrößert.