Exercise 3.2Z: Optimum Cutoff Frequency for Gaussian Low-pass
Wie in Aufgabe A3.2 wird ein binäres bipolares redundanzfreies Binärsystem mit gaußförmigen Empfangsfilter $H_G(f)$ betrachtet. Dessen Grenzfrequenz $f_G$ soll so bestimmt werden, dass das ungünstigste S/N–Verhältnis
- $$\rho_{\rm U} = \frac{[\ddot{o}(T_{\rm D})/2]^2}{ \sigma_d^2}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} p_{\rm U} = {\rm Q} \left( \sqrt{\rho_{\rm U}} \right)$$
maximal und damit die ungünsigste Fehlerwahrscheinlichkeit $p_U$ minimal wird. Die so optimierte Grenzfrequenz $f_{\rm G, \ opt}$ führt meist zur minimalen mittleren Symbolfehlerwahrscheinlichkeit $p_{\rm S, \ min}$.
In obiger Gleichung sind folgende Systemgrößen verwendet:
- $\sigma_d^2$ ist die Detektionsrauschleistung. Bei gaußförmigen Empfangsfilter:
- $$\sigma_d^2 = \frac{N_0}{2} \cdot \int_{-\infty}^{+\infty} |H_{\rm G}(f)|^2 \,{\rm d} f = \frac{N_0 \cdot f_{\rm G}}{\sqrt{2}}\hspace{0.05cm}.$$
- $\ddot{o}(T_D)$ gibt die Augenöffnung an. Der Detektionszeitpunkt wird stets zu $T_D = 0$ angenommen.
- Bei einem gaußförmigen Empfangsfilter kann die vertikale Augenöffnung $\ddot{o}(T_D)$ allein durch die Amplitude $s_0$ des Sendegrundimpulses (obere Begrenzung im Auge ohne Rauschen) sowie durch den Maximalwert $g_0$ des Detektionsgrundimpulses ausgedrückt werden. Die Impulsamplitude $g_0$ ist dabei wie folgt zu berechnen:
- $$g_0 = g_d(t = 0) = s_0 \cdot \left [1- 2 \cdot {\rm Q} \left( \sqrt{2\pi} \cdot f_{\rm G} \cdot T \right)\right]\hspace{0.05cm}.$$
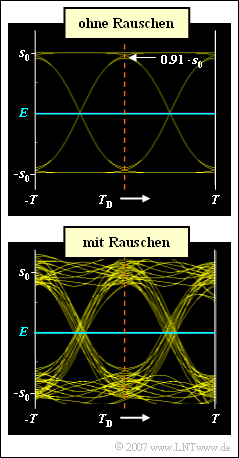
Die Grafik zeigt die Augendiagramme der gesuchten Konfiguration mit optimaler Grenzfrequenz. Im oberen Diagramm sind die Rauschstörungen nicht berücksichtigt. Das untere Diagramm gilt dagegen mit AWGN–Rauschen für $10 \cdot \rm lg \ E_B/N_0 = 10 \ \rm dB$.
Hinweise:
- Die Aufgabe bezieht sich auf das Kapitel Grundlagen der codierten Übertragung.
- Verwenden Sie zur numerischen Auswertung der Q–Funktion das folgende Interaktionsmodul: Komplementäre Gaußsche Fehlerfunktionen
Fragebogen
Musterlösung