Exercise 3.8Z: Optimal Detection Time for DFE
Wir betrachten wie in der Aufgabe A3.8 das bipolare Binärsystem mit Entscheidungsrückkopplung. Man nennt dies englisch Decision Feedback Equalization (DFE).
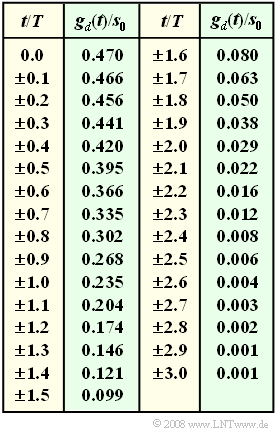
Der vorentzerrte Grundimpuls $g_d(t)$ am Eingang der DFE entspricht der Rechteckantwort eines Gaußtiefpasses mit der Grenzfrequenz $f_{\rm G} \cdot T = 0.25$.
In der Tabelle sind die auf $s_0$ normierten Abtastwerte von $g_d(t)$ angegeben. Auf der Angabenseite zu Aufgabe A3.8 ist $g_d(t)$ skizziert.
Bei der idealen DFE wird ein Kompensationsimpuls $g_w(t)$ gebildet, der für alle Zeiten $t ≥ T_{\rm D} + T_{\rm V}$ genau gleich dem Eingangsimpuls $g_d(t)$ ist, so dass für den korrigierten Grundimpuls gilt:
- $$g_k(t) \ = \ g_d(t) - g_w(t) =$$
- $$\ = \\left\{ \begin{array}{c} g_d(t) $$
- $$ 0 $$
- $$ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}$$
- $$ {\rm{f\ddot{u}r}} $$
- $$\end{array} \begin{array}{*{20}c} t < T_{\rm D} + T_{\rm V}, $$
- $$ t \ge T_{\rm D} + T_{\rm V}, $$
- $$\end{array}$$
- $$g_k(t) \ = \ g_d(t) - g_w(t) =\\ \ = \ \left\{ \begin{array}{c} g_d(t) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ {\rm{f\ddot{u}r}} \\ \end{array} \begin{array}{*{20}c} t < T_{\rm D} + T_{\rm V}, \\ t \ge T_{\rm D} + T_{\rm V}, \\ \end{array}$$
Hierbei bezeichnet $T_{\rm D}$ den Detektionszeitpunkt, der eine optimierbare Systemgröße darstellt. $T_{\rm D} = 0$ bedeutet eine Symboldetektion in Impulsmitte.
Bei einem System mit DFE ist jedoch $g_k(t)$ stark unsymmetrisch, so dass ein Detektionszeitpunkt $T_{\rm D} < 0$ günstiger ist. Die Verzögerungszeit $T_{\rm V} = T/2$ gibt an, dass die DFE erst eine halbe Symboldauer nach der Detektion wirksam wird. Zur Lösung dieser Aufgabe ist $T_{\rm V}$ allerdings nicht relevant.
Fragebogen
Musterlösung