Exercise 3.09: Correlation Receiver for Unipolar Signaling
Betrachtet wird die gemeinsame Entscheidung von $N = 3$ Binärsymbolen (Bit) mittels des Korrelationsempfängers. Die $M = 8$ möglichen Quellensymbolfolgen $Q_i$ besitzen alle die gleiche Wahrscheinlichkeit und sie sind durch die folgenden unipolaren Amplitudenkoeffizienten festgelegt:
- $$Q_0 = 000, \hspace{0.15cm}Q_1 = 001,\hspace{0.15cm}Q_2 = 010,\hspace{0.15cm}Q_3 = 011 \hspace{0.05cm},$$
- $$Q_4 = 100, \hspace{0.15cm}Q_5 = 101,\hspace{0.15cm}Q_6 = 110,\hspace{0.15cm}Q_7 = 111 \hspace{0.05cm}.$$
Die möglichen Sendesignale $s_i(t)$ – jeweils mit der Dauer $3T$ – sind alle rechteckförmig mit Ausnahme von $s_0(t) = 0$. Die Signale $s_1(t)$, $s_2(t)$, und $s_4(t)$ mit nur jeweils einer „$1$” besitzen die Signalenergie $E_{\rm B}$ (steht für „Energie pro Bit”), während zum Beispiel die Energie von $s_7(t)$ gleich $3E_{\rm B}$ beträgt.
Der Korrelationsempfänger bildet aus dem verrauschten Empfangssignal $r(t) = s(t) + n(t)$ insgesamt $2^3 = 8$ Entscheidungsgrößen (Metriken)
- $$W_i = I_i - {E_i}/{2 }\hspace{0.3cm}{\rm mit}\hspace{0.3cm} I_i =\int_{0}^{3T} r(t) \cdot s_i(t) \,{\rm d} t \hspace{0.3cm}( i = 0, ... , 7)$$
und setzt die Sinkensymbolfolge $V = Q_j$, falls $W_j$ größer ist als alle anderen $W_{\it i≠j}$. Damit trifft er eine optimale Entscheidung im Sinne von Maximum–Likelihood.
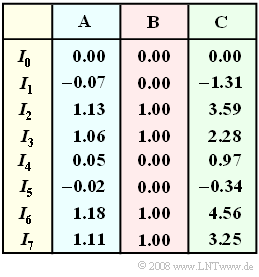
In der Tabelle sind die (unkorrigierten) Korrelationswerte $I_0, \ ... \ , I_7$ für drei verschiedene Systeme werden. Eine dieser Spalten steht für „keine Störung”, eine für „geringe Störungen” und eine weitere für „starke Störungen”. Zur Bestimmung der Metriken für die drei Systemvarianten wurde stets die gleiche Quellensymbolfolge gesendet.
Hinweis:
- Die Aufgabe gehört zum Themengebiet von Kapitel Optimale Empfängerstrategien dieses Buches.
Fragebogen
Musterlösung