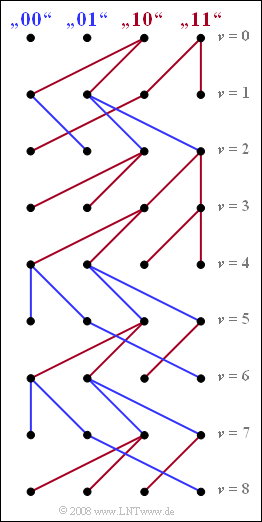
Exercise 3.12: Trellis Diagram for Two Precursors

• Return to book

Trellisdiagramm für 2 Vorläufer

Wir gehen von den Grundimpulswerten $g_0$, $g_{\rm –1}$ und $g_{\rm &ndash2}$ aus. Das bedeutet, dass die Entscheidung über das Symbol $a_{\rm \nu}$ auch durch die nachfolgenden Koeffizienten $a_{\rm \nu +1}$ und $a_{\rm \nu +2}$ beeinflusst wird. Damit sind für jeden Zeitpunkt $\nu$ genau $8$ Fehlergrößen $\epsilon_{\rm \nu}$ zu berechnen, aus denen die minimalen Gesamtfehlergrößen ${\it \Gamma}_{\rm \nu}(00)$, ${\it \Gamma}_{\rm \nu}(01)$, ${\it \Gamma}_{\rm \nu}(10)$ und ${\it \Gamma}_{\rm \nu}(11)$ berechnet werden können. Hierbei liefert beispielsweise ${\it \Gamma}_{\rm \nu}(01)$ Information über das Symbol $a_{\rm \nu}$ unter der Annahme, dass $a_{\rm \nu +1} = 0$ und $a_{\rm \nu +2} = 1$ sein werden. Die minimale Gesamtfehlergröße ${\it \Gamma}_{\rm \nu}(01)$ ist hierbei der kleinere Wert aus dem Vergleich von

$${\it \Gamma}_{\nu-1}(00) + \varepsilon_{\nu}(001) \hspace{0.15cm}{\rm und} \hspace{0.15cm}{\it \Gamma}_{\nu-1}(10) + \varepsilon_{\nu}(101).$$

Zur Berechnung der minimalen Gesamtfehlergröße ${\it \Gamma}_2(10)$ in den Teilaufgaben (1) und (2) soll von folgenden Zahlenwerten ausgegangen werden:

Fragebogen

1

Multiple-Choice Frage

	Falsch
	Richtig

2

Input-Box Frage

$\alpha$ =

Musterlösung

Solution

1. 2. 3. 4. 5. 6. 7.