Exercise 4.1: About the Gram-Schmidt Process

• Return to book

Zum Gram-Schmidt-Verfahren

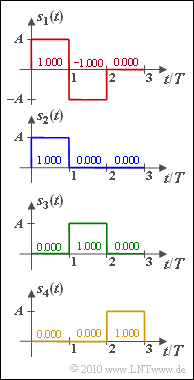
Für die vier durch die Abbildung definierten Signale $s_1(t), \, ... \, , s_4(t)$ sind durch Anwendung des sog. Gram–Schmidt–Verfahrens die drei sich ergebenden Basisfunktionen $\varphi_1(t)$, $\varphi_2(t)$ und $\varphi_3(t)$ zu ermitteln, so dass für die Signale mit $i = 1, \, ... \, , \ 4$ geschrieben werden kann:

$$s_i(t) = s_{i1} \cdot \varphi_1(t) + s_{i2} \cdot \varphi_2(t) + s_{i3} \cdot \varphi_3(t)\hspace{0.05cm}.$$

In der Teilaufgabe (1) gelte $A^2 = 1 \ \rm mW$ und $T = 1 \ \rm \mu s$. In den späteren Teilaufgaben sind die Amplitude und die Zeit jeweils normierte Größen:$A = 1$, $T = 1$. Damit sind sowohl die Koeffizienten $s_{\it ij}$ als auch die Basisfunktionen $\varphi_{\it}(t)$ – jeweils mit $j = 1, 2, 3$ – dimensionslose Größen.

Hinweise:

• Die Aufgabe bezieht sich inhaltlich auf das Kapitel Signale, Basisfunktionen und Vektorräume.
• Auf der Seite 3a des Kapitels ist das Gram–Schmidt–Verfahren angegeben, auf der Seite 3b finden Sie ein Berechnungsbeispiel ähnlich zu dieser Aufgabe.

Fragebogen

1

Multiple-Choice Frage

	Falsch
	Richtig

2

Input-Box Frage

$\alpha$ =

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)  (6)