Exercise 1.4: Nyquist Criteria
From LNTwww
Rechteckförmiges Nyquistspektrum
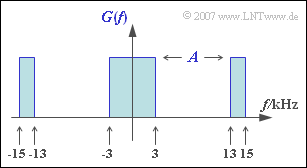
Durch die Skizze gegeben ist das Spektrum $G(f)$ des Detektionsgrundimpulses, wobei der Parameter $A$ noch zu bestimmen ist. Überprüft werden soll unter Anderem, ob dieser Detektionsgrundimpuls eines der beiden Nyquistkriterien erfüllt. Diese lauten:
- Das erste Nyquistkriterium ist erfüllt, wenn für die Spektralfunktion gilt:
- $$\sum_{k = -\infty}^{+\infty} G(f - \frac{k}{T} ) = {\rm const.}$$
In diesem Fall besitzt der Impuls $g(f)$ für alle ganzzahligen Werte von $ν$ mit Ausnahme von $ν = 0$ Nulldurchgänge bei $t = νT$. Für die gesamte Aufgabe wird $T = 0.1 \ \rm ms$ vorausgesetzt.
- Ist das zweite Nyquistkriterium erfüllt, so hat $g(f)$ Nulldurchgänge bei $\pm 1.5 T$, $\pm 2.5 T$, usw.
Hinweis:
Die Aufgabe bezieht sich auf den Theorieteil von Eigenschaften von Nyquistsystemen dieses Buches. Als bekannt vorausgesetzt werden:
- $$X(f) = \left\{ \begin{array}{c} A \\ 0 \\\end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\hspace{0.15cm}|f| < f_0 \hspace{0.05cm}, \\ {\rm{f\ddot{u}r}}\hspace{0.15cm}|f| > f_0 \hspace{0.08cm} \\ \end{array} \hspace{0.4cm}\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm} x(t) =2 \cdot A \cdot f_0 \cdot {\rm si}(2 \pi f_0 T) \hspace{0.05cm},$$
- $$\sin(\alpha) \cdot \cos (\beta) = \frac{1}{2} \cdot \left[ \sin(\alpha - \beta) + \sin(\alpha + \beta)\right] \hspace{0.05cm}.$$
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)
(6)
