Exercise 1.6: Root Nyquist System

• Return to book

Cosinus-Spektrum

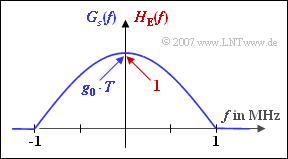
Die nebenstehende Grafik zeigt

• das Spektrum $G_{s}(f)$ des Sendegrundimpulses,
• den Frequenzgang $H_{\rm E}(f)$ des Empfangsfilters

eines binären und bipolaren Übertragungssystems, die zueinander formgleich sind:

$$G_s(f) = \left\{ \begin{array}{c} A \cdot \cos \left( \frac {\pi \cdot f}{2 \cdot f_2} \right) \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ \\ \end{array} \begin{array}{*{20}c}|f| \le f_2 \hspace{0.05cm}, \\ \\ {\rm sonst }\hspace{0.05cm}, \\ \end{array}$$

$$H_{\rm E }(f) = \left\{ \begin{array}{c} 1 \cdot \cos \left( \frac {\pi \cdot f}{2 \cdot f_2} \right) \\ \\ 0 \\ \end{array} \right.\quad \begin{array}{*{1}c} {\rm{f\ddot{u}r}}\\ \\ \\ \end{array} \begin{array}{*{20}c}|f| \le f_2 \hspace{0.05cm}, \\ \\ {\rm sonst }\hspace{0.05cm}. \\ \end{array}$$

In der gesamten Aufgabe gelte $A = 10^{–6} \ \rm V/Hz$ und $f_{2} = 1 \ \rm MHz$.

Unter der Voraussetzung, dass die Bitrate $R = 1/T$ richtig gewählt wird, erfüllt der Detektionsgrundimpuls $g_{d}(t) = g_{s}(t) ∗ h_{\rm E}(t)$ das erste Nyquistkriterium. Bei der dazugehörigen Spektralfunktion $G_{d}(f)$ erfolgt dabei der Flankenabfall cosinusförmig ähnlich einem Cosinus–Rolloff–Spektrum; der Rolloff–Faktor $r$ ist in dieser Aufgabe zu ermitteln.

Hinweis:

• Die Aufgabe bezieht sich auf das Optimierung der Basisbandübertragungssystemedieses Buches. Zahlenwerte der Q–Funktion liefert zum Beispiel das folgende Interaktionsmodul: Komplementäre Gaußsche Fehlerfunktionen
• Der Crestfaktor ist der Qotient aus Maximalwert und Effektivwert des Sendesignals und damit ein Maß für die sendeseitigen Impulsinterferenzen:

$$C_{\rm S} = \frac{s_0}{\sqrt{E_{\rm B}/T}} = \frac{{\rm Max}[s(t)]}{\sqrt{{\rm E}[s^2(t)]}}= {s_0}/{s_{\rm eff}}.$$

Fragebogen

1

Berechnen Sie das Nyquistspektrum $G_{d}(f)$. Wie groß sind Nyquistfrequenz und Rolloff–Faktor?

$f_{\rm Nyq} \ = \ $ $\ \rm MHz$

$r \ = \ $

2

Wie groß ist die Bitrate des vorliegenden Nyquistsystems?

$R \ = \ $ $\ \rm Mbit/s$

3

Warum handelt es sich unter der Nebenbedingung „Leistungsbegrenzung” um ein optimales System?

	Das Gesamtsystem erfüllt die Nyquistbedingung.
	Der Crestfaktor ist $C_{\rm S} = 1$.
	Das Empfangsfilter ist an den Sendegrundimpuls angepasst.

4

Welche Bitfehlerwahrscheinlichkeit ergibt sich, wenn für die Leistungsdichte des AWGN–Rauschens $N_{0} = 8 \cdot 10^{–8}\ \rm V^{2}/Hz$ (bezogen auf $1 Ω$) gilt?

$p_{\rm B} \ = \ $ $\ \cdot 10^{-6}$

Musterlösung

Solution

(1)  (2)  (3)  (4)  (5)  (6)