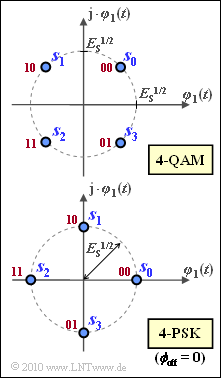
Exercise 4.14Z: 4-QAM and 4-PSK
Für die Quadraturamplitudenmodulation (M&ndashQAM) wurde im Theorieteil für $M ≥ 16$) eine obere Schranke („Union–Bound”) der Symbolfehlerwahrscheinlichkeit angegeben:
- $$ p_{\rm UB} = 4 \cdot {\rm Q} \left [ \sqrt{ { E_{\rm S}}/{ N_0}} \right ] \ge p_{\rm S} \hspace{0.05cm}.$$
Im Theorieteil findet man ebenfalls die „Union–Bound” für die M–stufige Phasenmodulation (M–PSK)
- $$ p_{\rm UB} = 2 \cdot {\rm Q} \left [ \sin ({ \pi}/{ M}) \cdot \sqrt{ { 2E_{\rm S}}/{ N_0}} \right ] \ge p_{\rm S} \hspace{0.05cm}.$$
Bei beiden Verfahren hat jeder Signalraumpunkt die genau gleiche Energie, nämlich $E_{\rm S}$.
Aus der Grafik erkennt man, dass für den Sonderfall $M = 4$ die beiden Modulationsverfahren eigentlich identisch sein müssten, was aus den obigen Gleichungen nicht direkt hervorgeht.
Die 4–PSK ist hier mit dem Phasenoffset $\phi_{\rm off} = 0$ dargestellt. Mit einem allgemeinen Phasenoffset lauten dagegen die Inphase– und Quadraturanteile der Signalraumpunkte allgemein ($i = 0, \ ... \ , M = 1$):
- $$s_{{\rm I}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm},$$
- $$ s_{{\rm Q}i} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sin \left ( { 2\pi i}/{ M} + \phi_{\rm off} \right ) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe bezieht sich auf die Theorieseite 6 und die Theorieseite 7 von Kapitel 4.4.
- In der obigen Grafik rot eingezeichnet ist die Gray–Zuordnung der Symbole zu Bitdupeln.
Fragebogen
Musterlösung