Exercise 2.3: Binary Signal and Quaternary Signal

• Return to book

AKF und LDS von Binärsignal und Quaternärsignal

Es sollen zwei redundanzfreie Übertragungssysteme B und Q jeweils mit bipolaren Amplitudenkoeffizienten $a_{\nu}$ vergleichend gegenübergestellt werden. Beide Systeme erfüllen die erste Nyquistbedingung. Gemäß der Wurzel–Wurzel–Aufteilung ist das Spektrum $G_{d}(f)$ des Detektionsgrundimpulses formgleich mit der spektralen Leistungsdichte ${\it \Phi}_{s}(f)$ des Sendesignals. Bekannt sind folgende Eigenschaften der beiden Systeme:

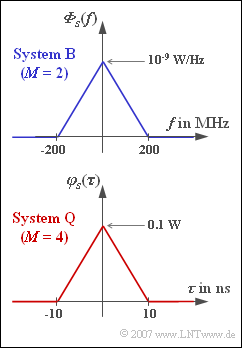
• Vom binären System B ist die spektrale Leistungsdichte ${\it \Phi}_{s}(f)$ am Sender bekannt und in der Grafik zusammen mit den Beschreibungsparametern dargestellt.
• Das System Q benutzt ein NRZ–Rechtecksignal mit den vier möglichen Amplitudenwerten $±s_{0}$ und $±s_{0}/3$, die alle mit gleicher Wahrscheinlichkeit auftreten.
• ${s_{0}}^{2}$ hat die Einheit einer Leistung und gibt die maximale Momentanleistung an, die nur dann auftritt, wenn eines der beiden „äußeren Symbole” gesendet wird.
• Die Beschreibungsparameter von System Q können der dreieckförmigen AKF in nebenstehender Grafik entnommen werden.

Hinweise:

• Die Aufgabe gehört zum Kapitel Grundlagen der codierten Übertragung.
• Bezug genommen wird auch auf das Kapitel Redundanzfreie Codierung .
• Berücksichtigen Sie, dass Autokorrelationsfunktion (AKF) und Leistungsdichtespektrum (LDS) eines stochastischen Signals stets über die Fouriertransformation zusammenhängen.
• Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

1

Welche Symboldauer $T$ hat das Binärsystem mit Nyquisteigenschaft?

System ${\rm B}: T \ = \ $ $\ \rm ns$

2

Wie groß ist die (äquivalente) Bitrate des Binärsystems?

System ${\rm B}: R_{\rm B} \ = \ $ $\ \rm Mbit/s$

3

Welche Leistung besitzt das binäre Sendesignal?

System ${\rm B}: P_{\rm S} \ = \ $ $\ \rm mW$

4

Welche Aussagen sind bezüglich des Binärsystems zutreffend?

	Die AKF $\varphi_{s}(\tau)$ des Sendesignals ist $\rm si^{2}$–förmig.
	Die Energie–AKF $\varphi^{^{\bullet}}_{gs}(\tau)$ des Grundimpulses ist $\rm si^{2}$–förmig.
	Der Sendegrundimpuls $g_{s}(t)$ selbst ist $\rm si^{2}$–förmig.

5

Welche Symboldauer weist das Quaternärsystem auf?

System ${\rm Q}: T \ = \ $ $\ \rm ns$

6

Wie groß ist die äquivalente Bitrate des Quaternärsignals?

System ${\rm Q}: R_{\rm B} \ = \ $ $\ \rm Mbit/s$

7

Welche Leistung besitzt das quaternäre Sendesignal?

System ${\rm Q}: P_{\rm S} \ = \ $ $\ \rm mW$

8

Welche maximale momentane Sendeleistung besitzt das Quaternärsignal?

System ${\rm Q}: {s_{0}}^{2} \ = \ $ $\ \rm mW$

Musterlösung

Solution

(1)  Die Nyquistfrequenz $f_{\rm Nyq} = 100 \ \rm MHz$ kann aus der Grafik abgelesen werden. Daraus folgt mit den Aussagen von Eigenschaften von Nyquistsystemen :

$$f_{\rm Nyq} = \frac{1 } {2 \cdot T} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} T = \frac{1 } {2 \cdot f_{\rm Nyq}} \hspace{0.15cm}\underline{ =5\,{\rm ns}}\hspace{0.05cm}.$$

(2)  Beim Binärsystem ist die Bitrate gleichzeitig der Informationsfluss und es gilt:

$$R_{\rm B} = {1 }/ { T} \hspace{0.15cm}\underline {= 200\,{\rm Mbit/s}}= 2 \cdot f_{\rm Nyq} \cdot{\rm bit}/{\rm Hz}\hspace{0.05cm}.$$

(3)  Die Sendeleistung ist gleich dem Integral über $\it \Phi_{s}(f)$ und kann als Dreiecksfläche berechnet werden:

$$P_{\rm S} = \ \int_{-\infty}^{+\infty} {\it \Phi}_s(f) \,{\rm d} f = 10^{-9} \frac{\rm W}{\rm Hz} \cdot 200\,\,{\rm MHz} \hspace{0.15cm}\underline { = 200\,\,{\rm mW}}.$$

(4)  Richtig sind die beiden ersten Aussagen. Die Fourierrücktransformierte des Leistungsdichtespektrums $\it \Phi_{s}(f)$ ergibt die $\rm si^{2}$–förmige AKF $\varphi_{s}(\tau)$. Allgemein gilt zudem folgender Zusammenhang:

$$\varphi_s(\tau) = \sum_{\lambda = -\infty}^{+\infty}{1}/{T} \cdot \varphi_a(\lambda)\cdot \varphi^{^{\bullet}}_{gs}(\tau - \lambda \cdot T)\hspace{0.05cm}.$$

Bei einem redundanzfreien Binärsystem gilt jedoch $\varphi_{a}(\lambda = 0) = 1$, während alle anderen diskreten AKF–Werte $\varphi_{a}(\lambda \neq 0)$ gleich $0$ sind. Somit hat auch die Energie–AKF einen $\rm si^{2}$–förmigen Verlauf:

$$\varphi^{^{\bullet}}_{gs}(\tau ) = T \cdot \varphi_s(\tau) \hspace{0.05cm}.$$

Hinweis: Energie–AKF und Energie–LDS werden in diesem Tutorial jeweils mit Punkt versehen.

Dagegen trifft die letzte Aussage nicht zu. Für die folgende Begründung nehmen wir vereinfachend an, dass $g_{s}(t)$ symmetrisch sei und somit $G_{s}(f)$ reell ist. Dann gilt:

$${\it \Phi}_{s}(f) = {1 }/ { T} \cdot |G_s(f)|^2\hspace{0.3cm}\Rightarrow \hspace{0.3cm}G_s(f) = \sqrt{{ T} \cdot {\it \Phi}_{s}(f)}\hspace{0.4cm} \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ \hspace{0.4cm}g_s(t) \hspace{0.05cm}.$$

Aufgrund der Quadratwurzel in der obigen Gleichung ist der Sendegrundimpuls $g_{s}(t)$ nicht $\rm si^{2}$–förmig im Gegensatz zum Detektionsgrundimpuls $g_{d}(t)$, der formgleich mit der Energie–AKF $\varphi^{^{\bullet}}_{gs}(\tau)$ und damit $\rm si^{2}$–förmig ist. Gleichzeitig gilt $\varphi^{^{\bullet}}_{gs}(\tau) = g_{s}(\tau) ∗ g_{s}(–\tau)$.

(5)  Die AKF $\varphi_{s}(\tau)$ ist auf den Bereich $|\tau| ≤ T$ begrenzt, wenn der Sendegrundimpuls ein NRZ–Rechteck ist. Somit ergibt sich aus der Grafik die Symboldauer $T \underline{= 10 \ \rm ns}$.

(6)  Beim Quaternärsignal ergibt sich wegen der doppelten Symboldauer der gleiche Informationsfluss wie beim obigen Binärsignal:

$$R_{\rm B} = {{\rm log_2(4)} }/ { T} \hspace{0.15cm}\underline {= 200\,\,{\rm Mbit/s}}\hspace{0.05cm}.$$

(7)  Die Sendeleistung ist gleich dem AKF–Wert bei $\tau = 0$ und kann aus der Grafik abgelesen werden:

$$P_{\rm S} = \hspace{0.15cm}\underline {100\,\,{\rm mW}}.$$

(8)  Beim redundanzfreien Quaternärsignal mit NRZ–Rechteckimpulsen gilt für die mittlere Sendeleistung:

$$P_{\rm S} = {1}/ { 4} \cdot \left [ (-s_0)^2 + (-s_0/3)^2 + (+s_0/3)^2 +(+s_0)^2 \right ] = {5}/ { 9} \cdot s_0^2$$

$$\Rightarrow \hspace{0.3cm}s_0^2 = {9}/ {5} \cdot P_{\rm S} = {9}/ {5} \cdot 100\,\,{\rm mW}\hspace{0.15cm}\underline { = 180\,\,{\rm mW}}\hspace{0.05cm}.$$