Exercise 4.15: Optimal Signal Space Allocation

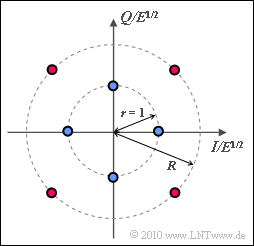
Betrachtete 8–QAM

Betrachtet wird hier eine Signalraumkonstellation mit $M = 8$ Signalraumpunkten:

Vier Punkte liegen auf einem Kreis mit Radius $r = 1$ .
Vier weitere Punkte liegen um $45^\circ$ versetzt auf einem zweiten Kreis mit Radius $R$ , wobei gelten soll:

$R_{\rm min} \le R \le R_{\rm max}\hspace{0.05cm},\hspace{0.2cm} R_{\rm min}= \frac{ \sqrt{3}-1}{ \sqrt{2}} \approx 0.518 \hspace{0.05cm},\hspace{0.2cm} R_{\rm max}= \frac{ \sqrt{3}+1}{ \sqrt{2}} \approx 1.932\hspace{0.05cm}.$

Die beiden Achsen (Basisfunktionen) seien jeweils normiert und werden vereinfachend mit $I$ und $Q$ bezeichnet. Zur weiteren Vereinfachung kann $E = 1$ gesetzt werden.

Im Fragebogen wird von blauen und roten Punkten gesprochen. Entsprechend der Grafik liegen die blauen Punkte auf dem Kreis mit Radius $r = 1$ , die roten auf dem Kreis mit Radius $R$ . Gezeichnet ist der Fall $R = R_{\rm max}$ .

Der Systemparameter $R$ soll in dieser Aufgabe so bestimmt werden, dass der Quotient

$\eta = \frac{ (d_{\rm min}/2)^2}{ E_{\rm B}}$

maximal wird. $\eta$ ist ein Maß für die Güte eines Modulationsalphabets bei gegebener Sendeenergie pro Bit (Power Efficiency). Es berechnet sich aus

der minimalen Distanz $d_{\rm min}$ , und
der Bitenergie $E_{\rm B}$ .

Es ist darauf zu achten, dass $d_{\rm min}^2$ und $E_{\rm B}$ in gleicher Weise normiert sind, was aber bereits durch die Aufgabenstellung implizit gegeben ist.

Hinweise:

Die Aufgabe gehört zum Kapitel Trägerfrequenzsysteme mit kohärenter Demodulation.
Bezug genommen wird insbesondere auf die Seiten Quadraturamplitudenmodulation und Mehrstufige Phasenmodulation.
Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.

Fragebogen

$R = 1 \text{:} \hspace{0.55cm} E_{\rm B}\ = \$

$R = \sqrt{2} \text{:} \hspace{0.2cm} E_{\rm B}\ = \$

	Für $R < R_{\rm min}$ tritt die minimale Distanz zwischen zwei roten Punkten auf.
	Für $R > R_{\rm max}$ tritt die minimale Distanz zwischen zwei blauen Punkten auf.
	Für $R_{\rm min} ≤ R ≤ R_{\rm max}$ tritt die minimale Distanz zwischen „Rot” und „Blau” auf.

$R = 1 \text{:} \hspace{0.55cm} d_{\rm min}\ = \$

$R = \sqrt{2} \text{:} \hspace{0.2cm} d_{\rm min}\ = \$

$\eta\ = \$

$R = R_{\rm min} \text{:} \hspace{0.35cm} \eta\ = \$

$R = R_{\rm max} \text{:} \hspace{0.2cm} \eta\ = \$

Musterlösung

Solution

(1) Wegen

$M = 8$ ⇒

$b = 3$ gilt für die mittlere Signalenergie pro Bit

$E_{\rm B} = E_{\rm S}/3$ , wobei die mittlere Signalenergie pro Symbol (

$E_{\rm S}$ ) als der mittlere quadratische Abstand der Signalraumpunkte vom Ursprung zu berechnen ist. Mit

$r = 1$ erhält man:

$E_{\rm S} = {1}/{8 } \cdot ( 4 \cdot r^2 + 4 \cdot R^2) = ({1 + R^2})/{2 } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} E_{\rm B} = {E_{\rm S}}/{3} = ({1 + R^2})/{6} \hspace{0.05cm}.$

Sonderfälle der 8–QAM

Insbesondere gilt:

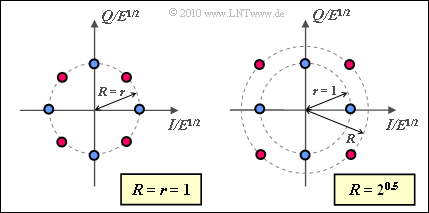
Für $R = 1$ ergibt sich eine 8–PSK und entsprechend $E_{\rm S} = 1$ und $E_{\rm B} \ \underline {= 1/3}$ (siehe linke Grafik).
Die rechte Grafik zeigt die Signalraumkonstellation für „Wurzel aus 2”. In diesem Fall ist $E_{\rm B} \ \underline {= 1/2}$ .

Anzumerken ist, dass diese Energien eigentlich noch mit der Normierungsenergie zu multiplizieren sind.

(2) Alle Aussagen treffen zu. Im gezeichneten Beispiel auf dem Angabenblatt mit $R = R_{\rm max}$ ist der Abstand zwischen zwei benachbarten blauen Punkten genau so groß wie der Abstand zwischen einem roten (äußeren) und einem blauen (inneren) Punkt. Für $R > R_{\rm max}$ ist der Abstand zwischen zwei blauen Punkten am geringsten. Für $R < R_{\rm min}$ tritt der minimale Abstand zwischen zwei roten Punkten auf.

(3)

Zur Berechnung der minimalen Distanz

Die Grafik verdeutlicht die geometrische Berechnung. Mit dem Satz von Pythagoras erhält man:

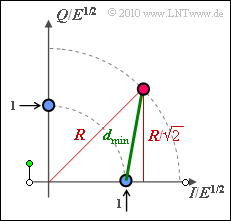
$d_{\rm min}^2 =(R/\sqrt{2})^2 + (R/\sqrt{2}-1)^2 = 1 - \sqrt{2} \cdot R + R^2$

$\Rightarrow \hspace{0.3cm}d_{\rm min} = \sqrt{ 1 - \sqrt{2} \cdot R + R^2} \hspace{0.05cm}.$

Insbesondere gilt für $R = 1$ (8–PSK):

$d_{\rm min} = \sqrt{ 2 - \sqrt{2} } \hspace{0.1cm} \underline{= 0.765} \hspace{0.1cm} (= 2 \cdot \sin (22.5^{\circ}) ) \hspace{0.05cm}.$

Dagegen ist für $\underline {R = „{\rm Wurzel \ aus \ 2}”}$ die minimale Distanz $d_{\rm min} \ \underline {= 1}$ (siehe rechte Grafik zur Teilaufgabe (1)).

(4) Mit den Ergebnissen der Teilaufgaben (1) und (3) erhält man allgemein bzw. für $R = 1$ (8–PSK):

$\eta = \frac{ d_{\rm min}^2}{ 4 \cdot E_{\rm B}} = \frac{ 1 - \sqrt{2} \cdot R + R^2}{ 4 \cdot (1 + R^2)/6} = \frac{ 3/2 \cdot(1 - \sqrt{2} \cdot R + R^2)}{ 1 + R^2}$

$\Rightarrow \hspace{0.3cm} R = 1: \hspace{0.2cm}\eta = \frac{ 3/2 \cdot(2 - \sqrt{2}) }{ 2} = 3/4 \cdot(2 - \sqrt{2})\hspace{0.1cm} \underline{\approx 0.439}\hspace{0.05cm}.$

(5) Für $R = R_{\rm min}$ ergibt sich folgender Wert:

$\eta = \frac{ 3/2 \cdot(1 - \sqrt{2} \cdot R + R^2)}{ 1 + R^2} = 3/2 \cdot \left [ 1 - \frac{ \sqrt{2} \cdot R }{ 1 + R^2}\right ]\hspace{0.05cm},$

$\sqrt{2} \cdot R = \sqrt{3}- 1\hspace{0.05cm},\hspace{0.2cm} 1 + R^2 = 3 - \sqrt{3} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \eta = 3/2 \cdot \left [ 1 - \frac{ \sqrt{3}- 1 }{ 3 - \sqrt{3}}\right ]\hspace{0.1cm} \underline{\approx 0.634}\hspace{0.05cm}.$

Für $R = R_{\rm max}$ ergibt sich genau der gleiche Wert.

Das (stets gewünschte) Maximum der Leistungseffizienz $\eta$ ergibt sich beispielsweise für $R = R_{\rm max}$ – also für die Signalraumkonstellation entsprechend dem Angabenblatt. In diesem Fall sind alle Dreiecke aus zwei benachbarten roten Punkten und dem dazwischenliegenden blauen Punkt gleichseitig. Auch für $R = R_{\rm min}$ ergeben sich gleichseitige Dreiecke, jetzt aber jeweils gebildet durch zwei blaue und einen roten Punkt. In diesem Fall ist zwar die Kantenlänge $d_{\rm min}$ deutlich kleiner, aber gleichzeitig ergibt sich auch ein kleineres $E_{\rm B}$ , so dass die Leistungseffizienz $\eta$ den gleichen Wert besitzt.

Die vorher betrachteten Sonderfälle $R = 1$ (8–PSK, linke Grafik zur Teilaufgabe (1)) und $R = 2^{\rm 0.5}$ (rechte Grafik) weisen mit $\eta = 0.439$ bzw. $\eta = 0.5$ (gegenüber $\eta = 0.634$ ) ein merklich kleineres $\eta$ auf.