Exercise 3.2Z: (3, 1, 3) Convolutional Encoder

Faltungscoder mit $k = 1, \ n = 3$ und $m = 3$

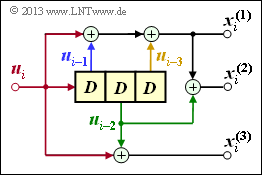
Der dargestellte Faltungscodierer wird durch die Parameter $k = 1$ (nur eine Informationssequenz $\underline{u}$) sowie $n = 3$ (drei Codesequenzen $\underline{x}^{(1)}, \ \underline{x}^{(2)}, \ \underline{x}^{(3)}$) charakterisiert. Aus der Anzahl der Speicherzellen ergibt sich das Gedächtnis $m = 3$.

Mit dem Informationsbit $u_i$ zum Codierschritt $i$ erhält man die folgenden Codebits:

$$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-3}\hspace{0.05cm},$$

$$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-2} + u_{i-3} \hspace{0.05cm},$$

$$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-2} \hspace{0.05cm}.$$

Daraus lassen sich Teilmatrizen $\mathbf{G}_l$ ableiten, wie auf der Theorieseite 1 dieses Kapitels beschrieben. Für die Generatormatrix kann somit geschrieben werden:

$$ { \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \ddots & \ddots & & & \ddots \end{pmatrix}\hspace{0.05cm},$$

und für die Codesequenz $\underline{x} = (x_1^{(1)}, \ x_1^{(2)}, \ x_1^{(3)}, \ x_2^{(1)}, \ x_2^{(2)}, \ x_2^{(3)}, \ ...)$ gilt:

$$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$

Hinweis:

Die Aufgabe gehört zum Kapitel Algebraische und polynomische Beschreibung.

Fragebogen

Musterlösung

Solution

(1) (2) (3) (4) (5)

	correct
	false