Exercise 3.2Z: (3, 1, 3) Convolutional Encoder
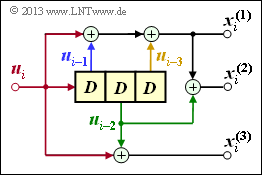
Der dargestellte Faltungscodierer wird durch die Parameter $k = 1$ (nur eine Informationssequenz $\underline{u}$) sowie $n = 3$ (drei Codesequenzen $\underline{x}^{(1)}, \ \underline{x}^{(2)}, \ \underline{x}^{(3)}$) charakterisiert. Aus der Anzahl der Speicherzellen ergibt sich das Gedächtnis $m = 3$.
Mit dem Informationsbit $u_i$ zum Codierschritt $i$ erhält man die folgenden Codebits:
- $$x_i^{(1)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-3}\hspace{0.05cm},$$
- $$x_i^{(2)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-1} + u_{i-2} + u_{i-3} \hspace{0.05cm},$$
- $$x_i^{(3)} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} u_{i} + u_{i-2} \hspace{0.05cm}.$$
Daraus lassen sich Teilmatrizen $\mathbf{G}_l$ ableiten, wie auf der Theorieseite 1 dieses Kapitels beschrieben. Für die Generatormatrix kann somit geschrieben werden:
- $$ { \boldsymbol{\rm G}}=\begin{pmatrix} { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & & & \\ & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m & &\\ & & { \boldsymbol{\rm G}}_0 & { \boldsymbol{\rm G}}_1 & { \boldsymbol{\rm G}}_2 & \cdots & { \boldsymbol{\rm G}}_m &\\ & & & \ddots & \ddots & & & \ddots \end{pmatrix}\hspace{0.05cm},$$
und für die Codesequenz $\underline{x} = (x_1^{(1)}, \ x_1^{(2)}, \ x_1^{(3)}, \ x_2^{(1)}, \ x_2^{(2)}, \ x_2^{(3)}, \ ...)$ gilt:
- $$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} \hspace{0.05cm}.$$
Hinweis:
- Die Aufgabe gehört zum Kapitel Algebraische und polynomische Beschreibung.
Fragebogen
Musterlösung
(2) Jede Teilmatrix $\mathbf{G}_l$ besteht aus einer Zeile ⇒ $k = 1$ und drei Spalten ⇒ $n = 3$.
(3) Alle Aussagen sind richtig. Da das aktuelle Informationsbit $u_i$ alle drei Ausgänge $x_i^{(1)}, \ x_i^{(2)}$ und $x_i^{(3)}$ beeinflusst, ist $\mathbf{G}_0 = (1, 1, 1)$. Dagegen sagt $\mathbf{G}_3 = (1, 1, 0)$ aus, dass nur die beiden ersten Eingänge von $u_{i–3}$ beeinflusst werden, nicht aber $x_i^{(3)}$.
(4) Die gesuchte Generatormatrix $\mathbf{G}$ ist nachfolgend dargestellt, wobei die vier Teilmatrizen $\mathbf{G}_0, \ ... , \mathbf{G}_3$ farblich unterschieden sind. Die Vektorgleichung
- $$\underline{x} = \underline{u} \cdot { \boldsymbol{\rm G}} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1) \cdot { \boldsymbol{\rm G}} $$
liefert das Ergebnis entsprechend dem Lösungsvorschlag 2. Die Codesequenz $\underline{x}$ ist dabei gleich der Modulo–2–Summe der Matrixzeilen 1, 3 und 4.
Farblich unterschieden sind die drei Codesequenzen der einzelnen Zweige. Beispielsweise gilt für den unteren Ausgang:
- $$\underline{x}^{(3)} = (1\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 0\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} 1\hspace{0.05cm},\hspace{0.05cm} ... \hspace{0.05cm}) \hspace{0.05cm}.$$
Anhand der vorne angegebenen Gleichungen kann dieses Resultat verifiziert werden:
- $${x}_1^{(3)} \hspace{-0.15cm} & = & \hspace{-0.15cm} u_1 + u_{-1} = 1+ (0) = 1 \hspace{0.05cm},\\ {x}_2^{(3)} \hspace{-0.15cm} & = & \hspace{-0.15cm} u_2 + u_{0} = 0+ (0) = 0 \hspace{0.05cm},\\ {x}_3^{(3)} \hspace{-0.15cm} & = & \hspace{-0.15cm} u_3 + u_{1} = 1+1 = 0 \hspace{0.05cm},\\ {x}_4^{(3)} \hspace{-0.15cm} & = & \hspace{-0.15cm} u_4 + u_{2} = 1+0 = 1 \hspace{0.05cm},\\ {x}_5^{(3)} \hspace{-0.15cm} & = & \hspace{-0.15cm} u_5 + u_{3} = 0+ 1 = 1 \hspace{0.05cm}.$$
Berücksichtigt ist hierbei die Speichervorbelegung mit Nullen: $u_0 = u_{–1} = 0$.
Anmerkung: Ist wie hier angenommen die Informationssequenz auf vier Bit begrenzt, so können in der Codesequenz Einsen bis zur Position $(4 + m) \cdot n = 21$ vorkommen.