Exercise 3.4: Systematic Convolution Codes
Man spricht von einem systematischen Faltungscode der Rate $R = 1/2$ ⇒ $k = 1, \ n = 2$, wenn das Codebit $x_i^{(1)}$ gleich dem momentan anliegenden Informationsbit $u_i$ ist.
Die Übertragungsfunktionsmatrix eines solchen Codes lautet:
- $${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) \hspace{0.05cm}.$$
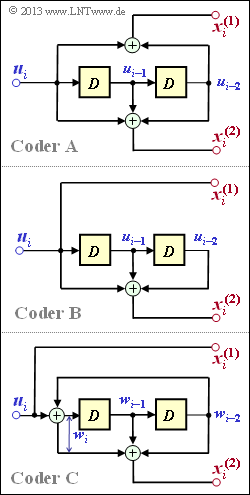
Der in der oberen Grafik dargestellte Coder A ist sicher nicht systematisch, da für diesen $G^{(1)}(D) ≠ 1$ gilt. Zur Herleitung der Matrix $\mathbf{G}(D)$ verweisen wir auf ein früheres Beispiel, in dem für unseren Standard–Rate–1/2–Coder mit Gedächtnis $m = 2$ ermittelt wurde:
- $${\boldsymbol{\rm G}}(D) \hspace{-0.15cm} & = & \hspace{-0.15cm} \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) =\\ & = & \hspace{-0.15cm} \big ( \hspace{0.05cm} 1 + D + D^2\hspace{0.05cm} , \hspace{0.2cm} 1 + D^2 \hspace{0.05cm}\big ) \hspace{0.05cm}.$$
Der Coder A unterscheidet sich gegenüber diesem Beispiel nur durch Vertauschen der beiden Ausgänge. Lautet die Übertragungsfunktionsmatrix eines Codes
- $${\boldsymbol{\rm G}}(D) = \big ( \hspace{0.05cm} G^{(1)}(D)\hspace{0.05cm} , \hspace{0.2cm} G^{(2)}(D) \hspace{0.05cm}\big ) \hspace{0.05cm},$$
so gilt für die äquivalente systematische Repräsentation dieses Rate–1/2–Faltungscodes allgemein:
- $${\boldsymbol{\rm G}}_{\rm sys}(D) = \big ( \hspace{0.05cm} 1\hspace{0.05cm} , \hspace{0.2cm} {G^{(2)}(D)}/{G^{(1)}(D)} \hspace{0.05cm}\big ) \hspace{0.05cm}.$$
In der Teilaufgabe (3) ist zu prüfen, welcher der systematischen Anordnungen (entweder Code B oder Code C oder auch beide) äquivalent zum Code A ist.
Hinweis:
- Die Aufgabe bezieht sich auf die Thematik von Kapitel 3.2.
Fragebogen
Musterlösung